Μαθήματα ενότητας

  • Η πρόσθεση και η αφαίρεση στους φυσικούς αριθμούς
  • Ο πολλαπλασιασμός στους φυσικούς αριθμούς
  • Πολλαπλάσια και διαιρέτες
  • Κριτήρια διαιρετότητας
  • Η διαίρεση στους φυσικούς αριθμούς

Η πρόσθεση και η αφαίρεση στους φυσικούς αριθμούς

Η πρόσθεση και η αφαίρεση στους φυσικούς αριθμούς

Βασικές μαθηματικές έννοιες και διεργασίες
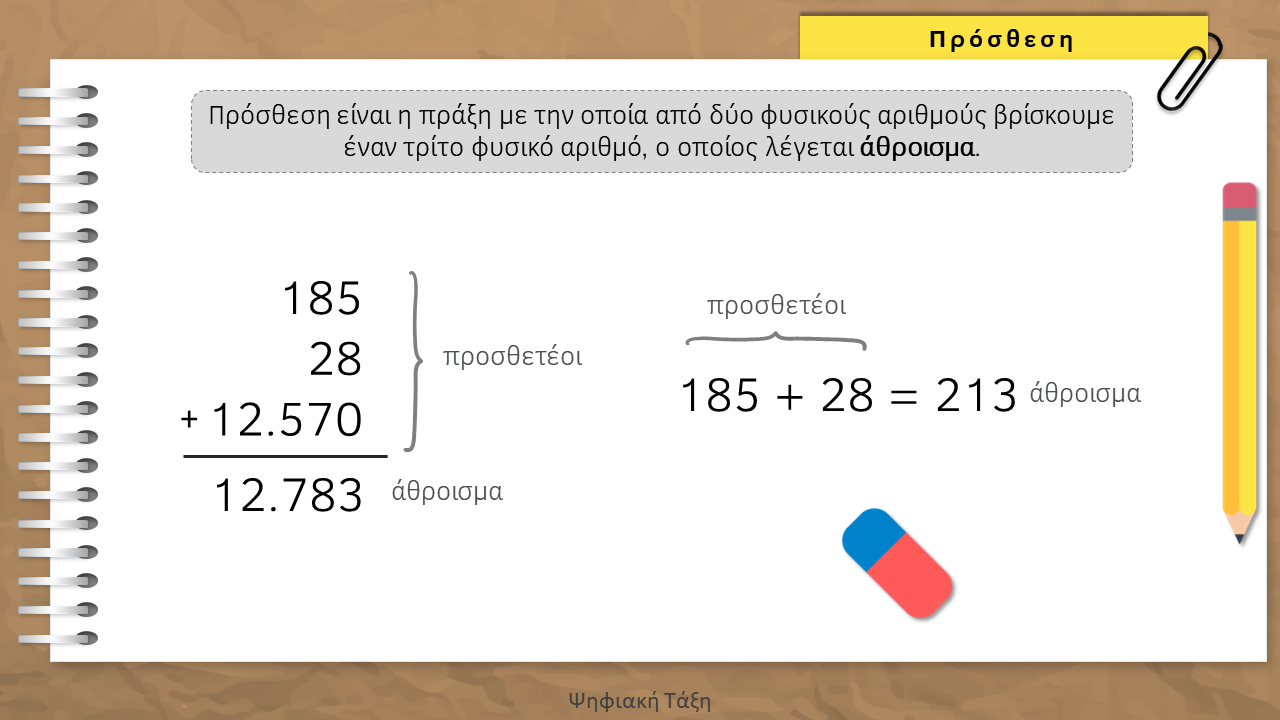
  • Πρόσθεση
  • Αφαίρεση
  • Ιδιότητες πρόσθεσης
<
>
  • Πρόσθεση είναι η πράξη με την οποία από δύο φυσικούς αριθμούς βρίσκουμε έναν τρίτο φυσικό αριθμό, ο οποίος λέγεται άθροισμα.
  • Οι αριθμοί οι οποίοι προστίθενται λέγονται προσθετέοι.
  • Αφαίρεση είναι η πράξη με την οποία από δύο φυσικούς αριθμούς, τον μειωτέο και τον αφαιρετέο, βρίσκουμε έναν τρίτο φυσικό αριθμό, που λέγεται διαφορά.
Αντιμεταθετική ιδιότητα: Αν αλλάξουμε τη σειρά των προσθετέων, το αποτέλεσμα της πρόσθεσης δεν αλλάζει.
Προσεταιριστική ιδιότητα: Για να προσθέσουμε πολλούς αριθμούς, προσθέτουμε τους δύο πρώτους, στο άθροισμά τους προσθέτουμε τον τρίτο, στο νέο άθροισμα προσθέτουμε τον τέταρτο κ.ο.κ.
Οι πράξεις της πρόσθεσης της αφαίρεσης είναι πράξεις αντίστροφες, γιατί:
​Μια πρόσθεση μπορεί να είναι η δοκιμή της αφαίρεσης.
​Μια αφαίρεση να είναι η δοκιμή της πρόσθεσης.

Ο πολλαπλασιασμός στους φυσικούς αριθμούς

Ο πολλαπλασιασμός στους φυσικούς αριθμούς

Βασικές μαθηματικές έννοιες και διεργασίες
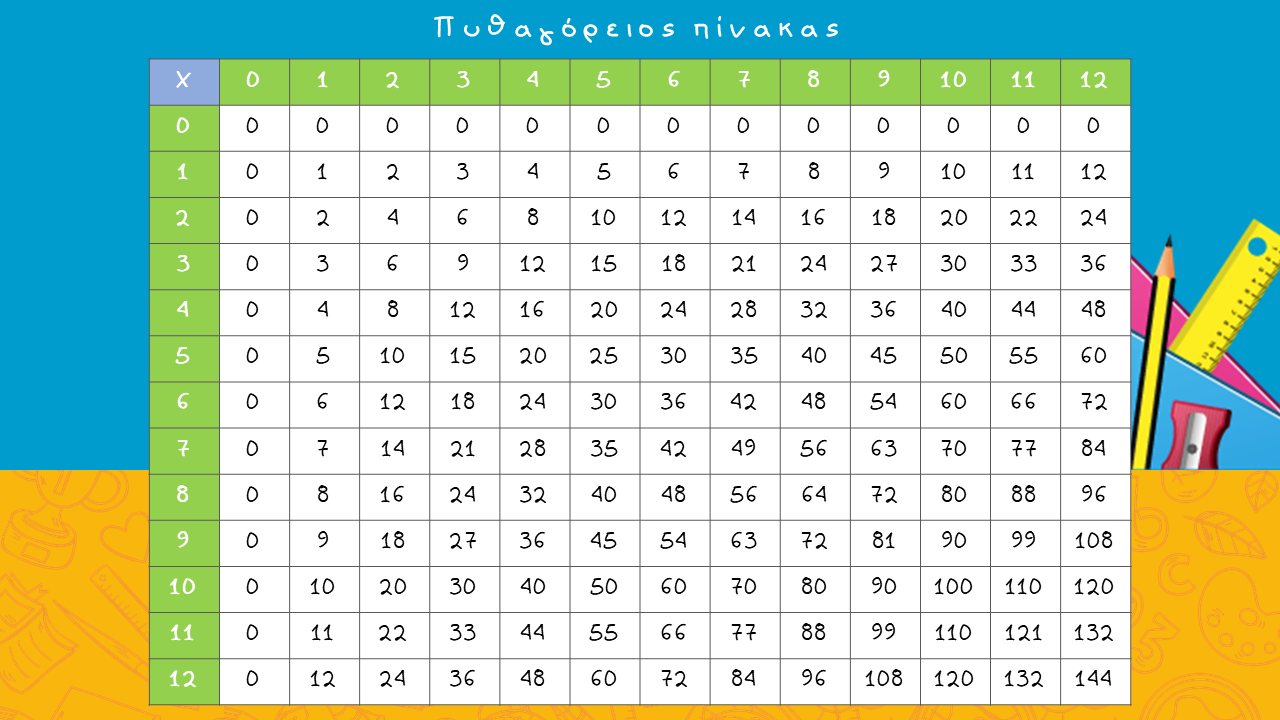
  • Πυθαγόρειος πίνακας
  • Πολλαπλασιασμός
<
>

Ο Πυθαγόρας και ο Πυθαγόρειος πίνακας

Στην αρχαία Ελλάδα ζούσε ο Πυθαγόρας, μεγάλος φιλόσοφος και μαθηματικός.  Γεννήθηκε σε χρονολογία που δεν μας είναι γνωστή, αλλά που εικάζεται πως είναι το 570 π.Χ. και ως επικρατέστερος τόπος γεννήσεως φέρεται η νήσος Σάμος. Είχε εφεύρει έναν «πίνακα», όπως τον έλεγε, που διευκόλυνε τους πολλαπλασιασμούς, οι οποίοι έως τότε γίνονταν με το μυαλό ή απλούστερα με πετραδάκια.
Μας φαίνεται τόσο απλό πράγμα! Ωστόσο, ο Πυθαγόρας αφιέρωσε είκοσι ολόκληρα χρόνια της ζωής του, ώσπου να επινοήσει αυτόν τον πίνακα, ο οποίος έκανε αθάνατο το όνομά του στους κατοπινούς αιώνες.
  • Πολλαπλασιασμός είναι η πράξη με την οποία από δύο φυσικούς αριθμούς βρίσκουμε έναν τρίτο φυσικό αριθμό, ο οποίος λέγεται γινόμενο των αριθμών αυτών.
  • Οι αριθμοί οι οποίοι πολλαπλασιάζονται λέγονται παράγοντες του γινομένου.
λυση προβληματοσ
4 x 250 € = 1.000 €
ΠΙΝΑΚΑΣ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΥ

Πίνακας πολλαπλασιασμού

Ο πολλαπλασιασμός είναι ένας γρήγορος τρόπος να κάνεις μια πρόσθεση που επαναλαμβάνεται ξανά και ξανά.
Πρόσθεση: 3 + 3 + 3 + 3 + 3 = 15  Πολλαπλασιασμός: 3 Χ 5 = 15 ​
ΣΤΑ ΠΕΝΑΛΤΙ - ΕΞΑΣΚΗΣΗ ΣΤΟΝ ΠΟΛΛΑΠΛΑΣΙΑΣΜΟ ​

Πολλαπλάσια και διαιρέτες

Πολλαπλάσια και διαιρέτες

Βασικές μαθηματικές έννοιες και διεργασίες
  • Πολλαπλάσια
  • Διαιρέτες
  • Ε.Κ.Π.
  • Μ.Κ.Δ.
<
>
Πολλαπλάσια ενός φυσικού αριθμού είναι όλοι οι αριθμοί που σχηματίζονται από τον πολλαπλασιασμό του με όλους τους φυσικούς αριθμούς.
Παράδειγμα:
Τα πολλαπλάσια του 4 είναι το 4, 8, 12, 16…
​4x2=8, 4x3=12, 4x4=16
Τα πολλαπλάσια κάθε αριθμού είναι άπειρα, διότι άπειροι είναι και οι αριθμοί με τους οποίους μπορώ να τον πολλαπλασιάσω.
Διαιρέτες ενός φυσικού αριθμού είναι κάθε άλλος αριθμός φυσικός αριθμός που τον διαιρεί τέλεια. 
  • Όλοι οι φυσικοί αριθμοί έχουν διαιρέτες τουλάχιστον το 1 και τον εαυτό τους.
  • Ένας αριθμός μπορεί να έχει πολλούς διαιρέτες.
  • Οι διαιρέτες ενός φυσικού αριθμού είναι μικρότεροι ή ίσοι του αριθμού.

Ελάχιστο Κοινό Πολλαπλάσιο (Ε.Κ.Π.)

Κοινά πολλαπλάσια (Κ.Π.) δύο ή περισσότερων αριθμών είναι τα πολλαπλάσια τα οποία είναι ίδια σε όλους τους αριθμούς
Παράδειγμα:
Π3 = 3, 6, 9, 12, 15, 18, 21, 24, 27, ...
Π4 = 4, 8, 12, 16, 20, 24, 28, ...
Π6 = 6, 12, 18, 24, 30, ...
Τα κοινά πολλαπλάσια του 3 του 4 και του 6, που είναι μικρότερα από το 30, είναι τα 12, 24.
Ελάχιστο Κοινό Πολλαπλάσιο (Ε.Κ.Π.) δύο ή περισσότερων αριθμών είναι το μικρότερο (ελάχιστο) από τα κοινά πολλαπλάσια των αριθμών.
πως βρισκουμε το ε.κ.π.
  • 1ος τρόπος
  • 2ος τρόπος
  • 3ος τρόπος
  • Βιντεομάθημα
<
>
  • Βρίσκουμε μερικά πολλαπλάσια των αριθμών.
  • Σημειώνουμε τα κοινά πολλαπλάσιά τους.
  • Επιλέγουμε το μικρότερο από αυτά.
​Παίρνουμε τον μεγαλύτερο αριθμό. Εξετάζουμε αν είναι πολλαπλάσιο ταυτόχρονα των άλλων. Εάν είναι, αυτός είναι και το Ε.Κ.Π.
Εάν δεν είναι, παίρνουμε τον διπλάσιό του και εξετάζουμε το ίδιο πράγμα.
Εάν δεν είναι και πάλι πολλαπλάσιο των άλλων, παίρνουμε τον τριπλάσιό του και ελέγχουμε ξανά. Συνεχίζουμε με τον ίδιο τρόπο, μέχρι να βρούμε ένα πολλαπλάσιο του μεγαλύτερου αριθμού που να είναι πολλαπλάσιο ταυτόχρονα και των άλλων αριθμών. Αυτό θα είναι και το Ε.Κ.Π.
  • Γράφω οριζόντια τους αριθμούς και δεξιά τους φέρνω μια κατακόρυφη γραμμή.
  • Δεξιά της γραμμής γράφω πρώτους αριθμούς (2,3,5,7,11…) που διαιρούν έστω και έναν από τους αριθμούς που έχουν δοθεί.
  • Τότε αριστερά της γραμμής, κάτω από τους αριθμούς που έχουν δοθεί, βάζω τα πηλίκα (όταν η διαίρεση είναι τέλεια) ή τον ίδιο αριθμό (όταν η διαίρεση δεν είναι τέλεια).
  • Συνεχίζω την ίδια διαδικασία μέχρι όλα τα πηλίκα να γίνουν 1.
  • Έτσι καταλήγουμε σε μια νέα γραμμή που όλα τα πηλίκα είναι μονάδες. Το Ε.Κ.Π. είναι το γινόμενο των αριθμών που βρίσκονται δεξιά της κατακόρυφης γραμμής

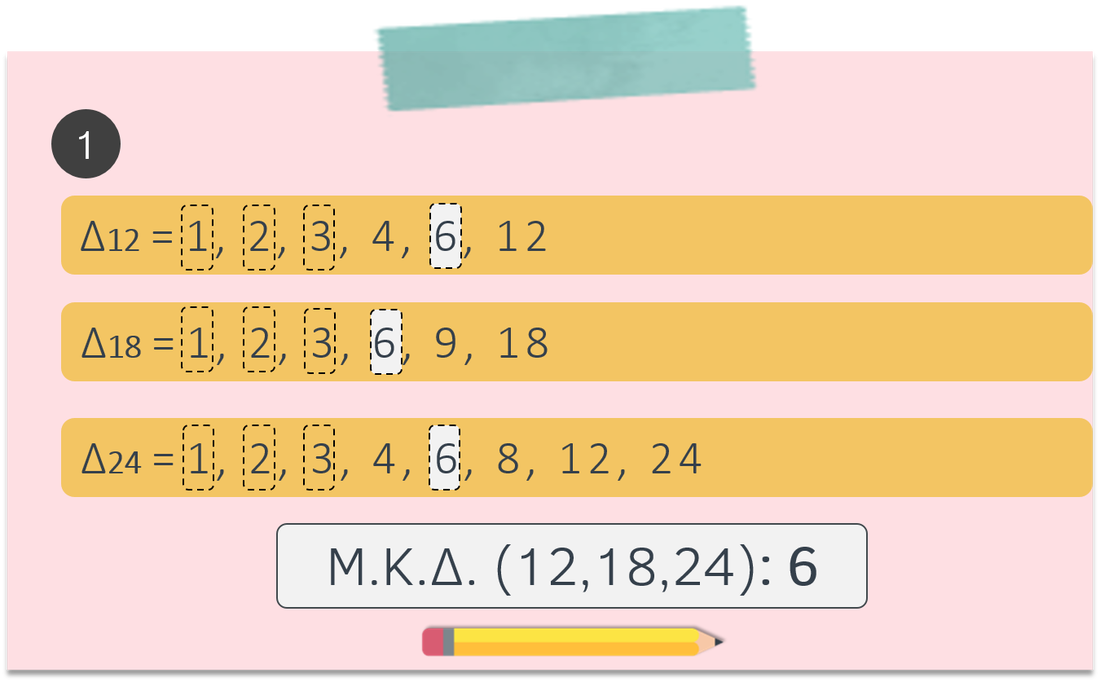
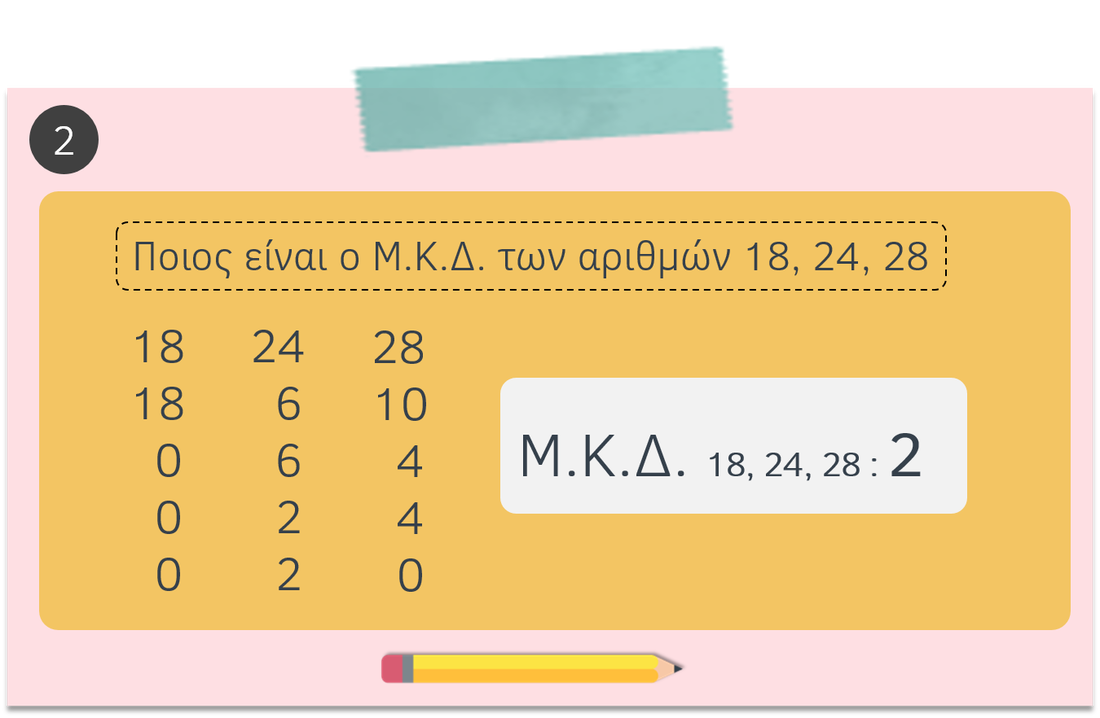
Μέγιστος Κοινός Διαιρέτης (Μ.Κ.Δ.)

  • Όλοι οι φυσικοί αριθμοί έχουν διαιρέτες τουλάχιστον το 1 και τον εαυτό τους.
  • Ένας αριθμός μπορεί να έχει πολλούς διαιρέτες.
  • Υπάρχουν αριθμοί που κάποιοι από τους διαιρέτες που έχουν είναι ίδιοι. Λέμε τότε ότι έχουν κοινούς διαιρέτες.
Μέγιστος Κοινός Διαιρέτης (Μ.Κ.Δ.) δύο ή περισσότερων αριθμών είναι ο μεγαλύτερος από τους κοινούς διαιρέτες των αριθμών αυτών.
πως βρισκουμε το μ.κ.δ.
  • 1ος τρόπος
  • 2ος τρόπος
  • Βιντεομάθημα
<
>
  • Βρίσκω τους διαιρέτες των αριθμών 12, 18 και 24.
  • Ξεχωρίζω τους κοινούς διαιρέτες: 1, 2, 3, και 6.
  • Ο μεγαλύτερος από τους κοινούς διαιρέτες (Μ.Κ.Δ.) είναι ο αριθμός 6.
  • Γράφω τους αριθμούς σε οριζόντια διάταξη, κατεβάζω το μικρότερο απ’ αυτούς (18) και τους διαιρώ με αυτόν.
  • Κάτω από κάθε αριθμό από τους άλλους γράφω το αντίστοιχο υπόλοιπο από τη διαίρεσή του (δηλαδή 6 κάτω από το 24 και 10 κάτω από το 28).
  • Κατεβάζω πάλι το μικρότερο από τους αριθμούς στη 2η σειρά τώρα (6) και διαιρώ τους υπόλοιπους με αυτόν.
  • Όταν μείνει μόνο ένας αριθμός και οι υπόλοιποι είναι 0, αυτός είναι ο Μ.Κ.Δ. Έτσι έχουμε Μ.Κ.Δ. (18, 24, 28) = 2

Κριτήρια διαιρετότητας

Κριτήρια διαιρετότητας

Βασικές μαθηματικές έννοιες και διεργασίες
  • του 2
  • του 3
  • του 5
  • του 9
  • του 10,100,1000
<
>
Ένας αριθμός διαιρείται με το 2 αν το τελευταίο ψηφίο είναι άρτιος (ζυγός) αριθμός (0,2,4,6,8). 
​Ένας αριθμός διαιρείται με το 3, αν το μονοψήφιο άθροισμα των ψηφίων του είναι 3, 6 ή 9.
​Ένας αριθμός διαιρείται με το 5 αν το τελευταίο ψηφίο είναι 0 ή 5.   
​ Ένας αριθμός διαιρείται με το 9 αν το μονοψήφιο άθροισμα των ψηφίων του είναι το 9.
​Ένας αριθμός διαιρείται με το:
  • το 10 όταν τελειώνει σε ένα τουλάχιστον 0
  • το 100 όταν τελειώνει σε δύο τουλάχιστον 0
  • το 1.000 όταν τελειώνει σε τρία τουλάχιστον 0
κριτηρια διαιρετοτητασ - εξασκηση

Η διαίρεση στους φυσικούς αριθμούς

Η διαίρεση στους φυσικούς αριθμούς

Βασικές μαθηματικές έννοιες και διεργασίες
Διαίρεση λέγεται η πράξη με την οποία μοιράζουμε έναν αριθμό σε τόσα ίσα μέρη, όσα μας λέει ένας άλλος αριθμός.
Έχουμε δυο ειδών διαιρέσεις:
  • Τη διαίρεση μερισμού. Όταν ξέρουμε την τιμή των πολλών μονάδων και ζητάμε την τιμή της μιας μονάδας.
        Π.χ. Οι πέντε σοκολάτες κοστίζουν 10 €. Πόσο κοστίζει η μία;
  • Τη διαίρεση μέτρησης. Όταν ξέρουμε και την τιμή των πολλών μονάδων και την τιμή της μιας μονάδας και δεν ξέρουμε πόσες είναι αυτές οι πολλές μονάδες.
        Π.χ. Αν έχω 12 κιλά μέλι και γεμίσω βάζα των 2 κιλών το καθένα. Πόσα βάζα χρησιμοποίησα;
  • Διαίρεση
  • ​Μαθαίνω
<
>
Όταν έχουμε δύο φυσικούς αριθμούς Δ και δ, τότε μπορούμε να βρούμε δύο άλλους μοναδικούς φυσικούς αριθμούς π και υ, έτσι ώστε να ισχύει: Δ = δ x π + υ.

​Ο αριθμός Δ ονομάζεται Διαιρετέος, ο δ διαιρέτης, ο π πηλίκο και ο υ υπόλοιπο της διαίρεσης.

Το υπόλοιπο είναι πάντα αριθμός μικρότερος από τον διαιρέτη και μεγαλύτερος ή ίσος του μηδενός.
  • Αν το υπόλοιπο υ είναι 0, τότε έχουμε μία Τέλεια Διαίρεση: Δ = δ x π
  • Η διαίρεση της μορφής Δ = δ x π + υ λέγεται Ευκλείδεια Διαίρεση.
  • Κάθε αριθμός αν διαιρεθεί με το 1, δίνει πηλίκο τον εαυτό του. 
​      π.χ. 5 : 1 = 5
  • Κάθε αριθμός αν διαιρεθεί με τον εαυτό του δίνει πηλίκο το 1.
      π.χ. 9 : 9 = 1
  • Το μηδέν (0) με όποιον αριθμό κι αν διαιρεθεί, δίνει πηλίκο τον εαυτό του.
​     π.χ. 0 : 5 = 0
  • Δεν επιτρέπεται να διαιρέσουμε έναν αριθμό δια μηδέν (0).
​     π.χ. 4 : 0 είναι αδύνατο
  • ​Σε κάθε διαίρεση αν πολλαπλασιάσουμε ή διαιρέσουμε τους δύο όρους με τον ίδιο αριθμό, το πηλίκο δεν αλλάζει.    
      π.χ. 20 : 4 = 5 (20 • 2) : (4 • 2) = 40 : 8 = 5

Επανάληψη ενότητας

Εξάσκηση - Quiz