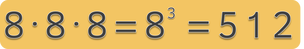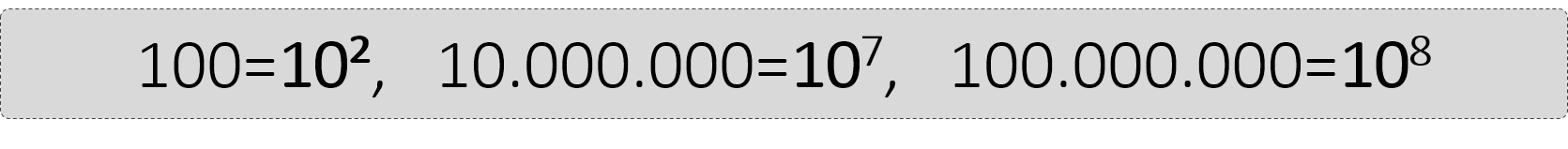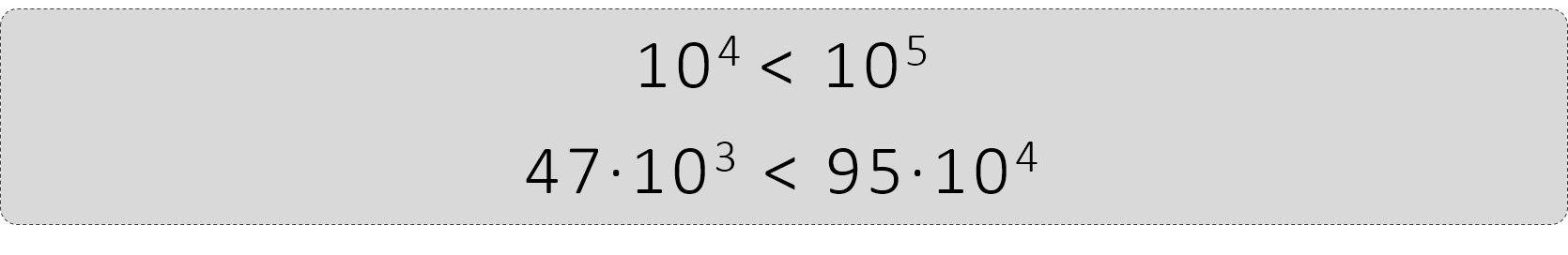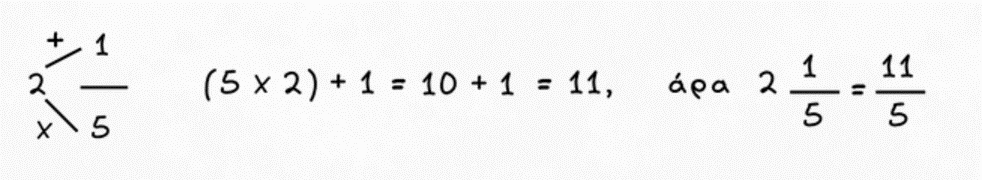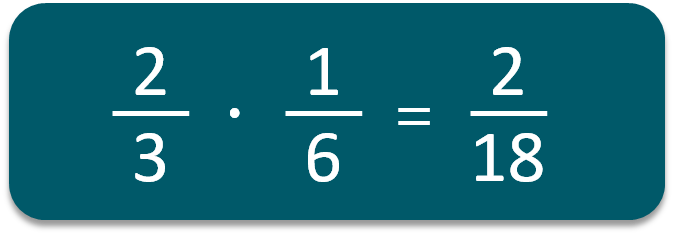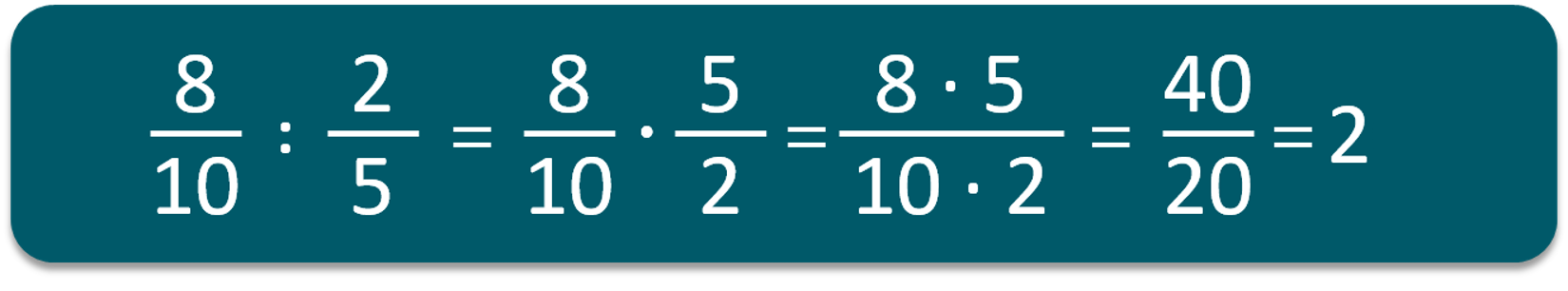Μαθήματα ενότητας
- Δυνάμεις
- Δυνάμεις του 10
- Κλάσματα ομώνυμα και ετερώνυμα
- Το κλάσμα ως ακριβές πηλίκο διαίρεσης
- Ισοδύναμα κλάσματα
- Σύγκριση - Διάταξη κλασμάτων
- Προβλήματα με πρόσθεση και αφαίρεση κλασμάτων
- Προβλήματα με πολλαπλασιασμό και διαίρεση κλασμάτων
Δυνάμεις
Δυνάμεις
Αποτελείται από δύο μέρη: Το 8, που λέγεται βάση της δύναμης και μας δείχνει ποιος αριθμός πολλαπλασιάζεται. Το 3, που λέγεται εκθέτης της δύναμης και μας δείχνει πόσες φορές πολλαπλασιάζεται η βάση της δύναμης. Ο εκθέτης γράφεται με μικρότερο μέγεθος, πάνω και δεξιά από τη βάση.
Δυνάμεις του 10
Δυνάμεις του 10
-
Σχηματίζουμε
-
Αναλύουμε
-
Γράφουμε
-
Συγκρίνουμε
<
>
Κλάσματα ομώνυμα και ετερώνυμα
Κλάσματα ομώνυμα και ετερώνυμα
Θυμάμαι ότι:
- Όταν ο αριθμητής είναι η μονάδα (το 1) και παρονομαστής οποιοσδήποτε αριθμός π.χ. 1/3 τότε το κλάσμα λέγεται κλασματική μονάδα.
- Ένα κλάσμα είναι ίσο με την ακέραια μονάδα, όταν έχει τον αριθμητή ίσο με τον παρονομαστή π.χ. 4/4.
- Όταν ο αριθμητής είναι μικρότερος του παρονομαστή π.χ. 2/5 τότε το κλάσμα λέγεται γνήσιο.
- Όταν ο αριθμητής είναι μεγαλύτερος από τον παρονομαστή π.χ. 5/2 τότε το κλάσμα λέγεται καταχρηστικό.
- Μεικτός αριθμός είναι αυτός που αποτελείται από ακέραιο και κλασματικό μέρος π.χ. 4 1/2.
Ομώνυμα λέγονται τα κλάσματα που έχουν τον ίδιο παρονομαστή.
Ετερώνυμα λέγονται τα κλάσματα που έχουνε διαφορετικούς παρονομαστές.
Ετερώνυμα λέγονται τα κλάσματα που έχουνε διαφορετικούς παρονομαστές.
βιντεομαθηματα
|
|
|
φυλλα εργασιασ
Το κλάσμα ως ακριβές πηλίκο διαίρεσης
Το κλάσμα ως ακριβές πηλίκο διαίρεσης
- Κάθε κλάσμα είναι ίσο με το πηλίκο μιας διαίρεση: (αριθμητής) : (παρονομαστή)
- Αντίστροφα κάθε διαίρεση μπορούμε να την εκφράσουμε και ως κλάσμα.
- Κάθε κλάσμα μπορεί να εκφραστεί ως δεκαδικός αν κάνουμε τη διαίρεση.
- Αν η διαίρεση είναι ατελής σταματάμε όπου μας χρειάζεται.
- Κάθε δεκαδικός μπορεί να μετατραπεί σε κλάσμα.
Πώς μετατρέπουμε ένα...
-
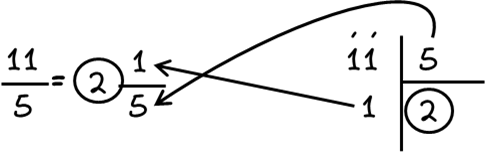
Καταχρηστικό κλάσμα σε μεικτό αριθμό
-
Μεικτό αριθμό σε κλάσμα
-
Εξάσκηση
<
>
Ισοδύναμα κλάσματα
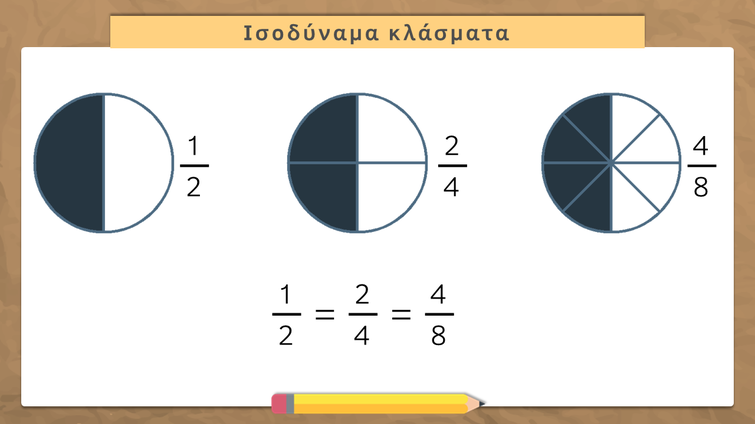
Ισοδύναμα κλάσματα
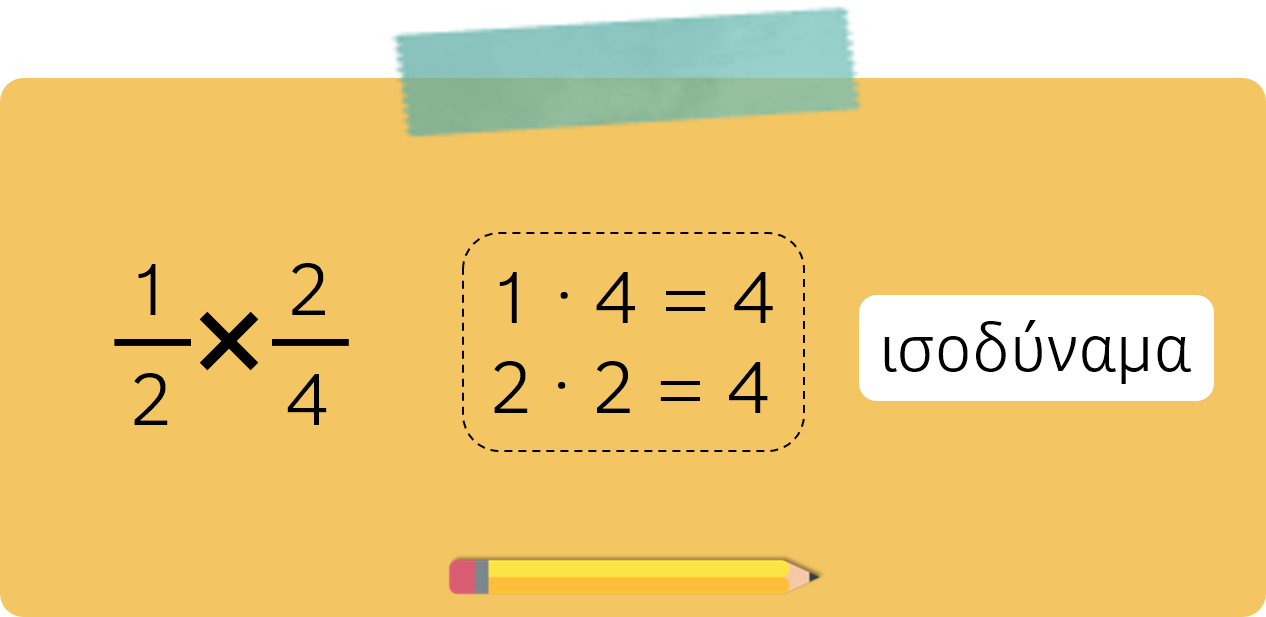
Δύο ή περισσότερα κλάσματα που έχουν διαφορετικούς όρους, δηλαδή διαφορετικό αριθμητή και παρονομαστή, αλλά εκφράζουν την ίδια ποσότητα, λέγονται ισοδύναμα.
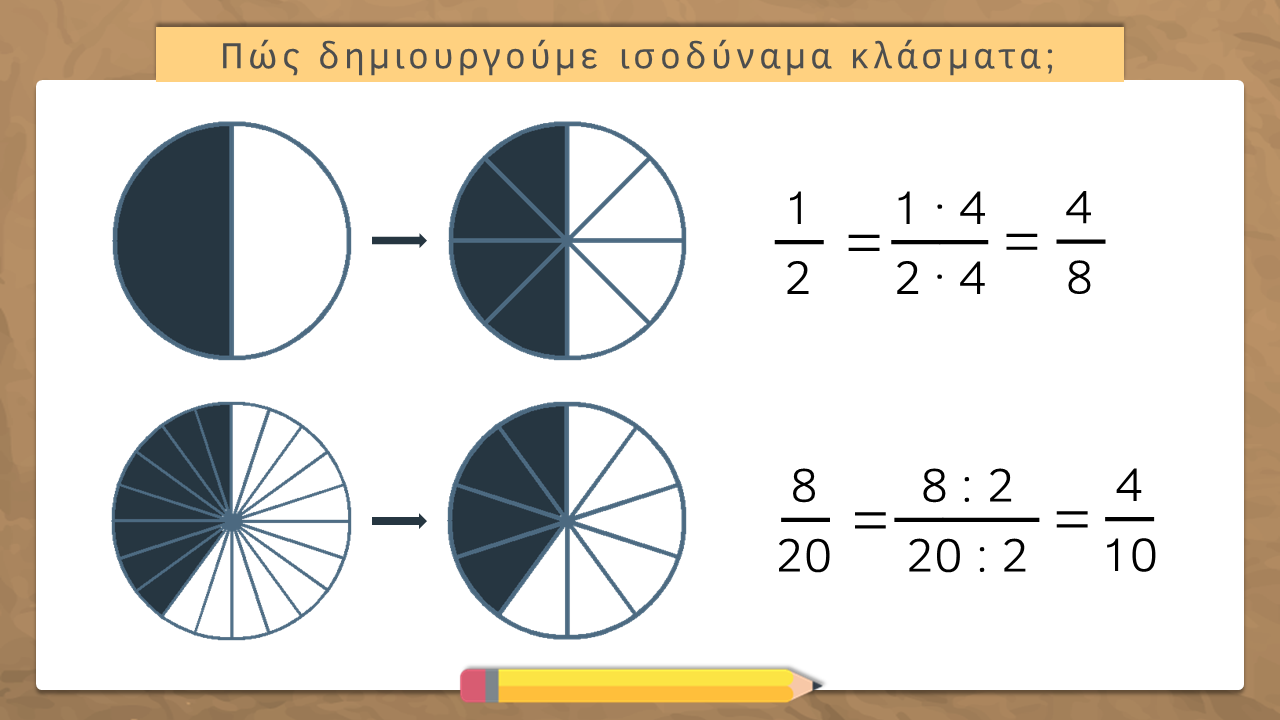
Πώς δημιουργούμε ισοδύναμα κλάσματα;
Για να δημιουργήσουμε ισοδύναμα κλάσματα πολλαπλασιάζουμε ή διαιρούμε και τους δύο όρους ενός κλάσματος με τον ίδιο αριθμό.
|
Όταν ένα κλάσμα δεν μπορεί να απλοποιηθεί, δεν υπάρχει δηλαδή αριθμός που να διαιρεί ακριβώς και τον αριθμητή και τον παρονομαστή, τότε το κλάσμα λέγεται ανάγωγο.
Για να απλοποιήσω ένα κλάσμα και να το κάνω ανάγωγο, χρησιμοποιώ το Μ.Κ.Δ. με τον οποίο διαιρώ και τους δύο όρους του κλάσματος.
Για να απλοποιήσω ένα κλάσμα και να το κάνω ανάγωγο, χρησιμοποιώ το Μ.Κ.Δ. με τον οποίο διαιρώ και τους δύο όρους του κλάσματος.
-
1ος τρόπος
-
2ος τρόπος
-
3ος τρόπος
<
>
ισοδυναμα κλασματα - bingo
φυλλα εργασιασ
Σύγκριση - Διάταξη κλασμάτων
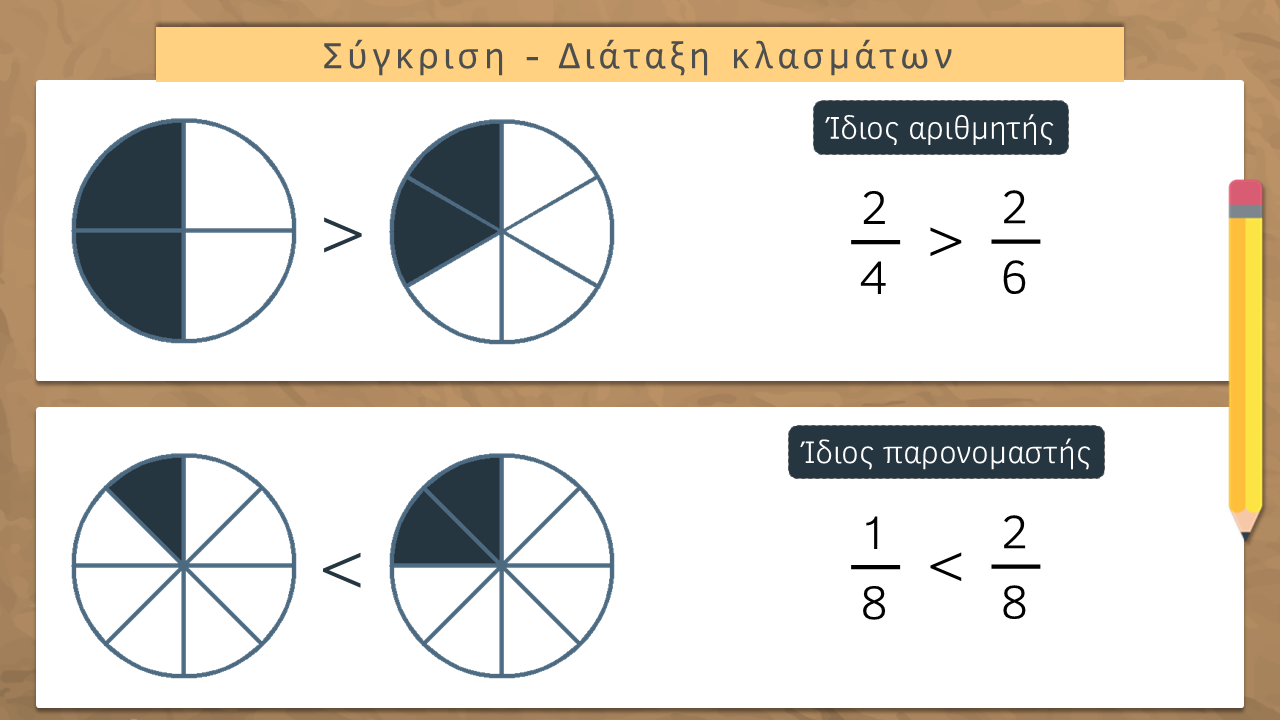
Σύγκριση - Διάταξη κλασμάτων
Τα κλάσματα αφού είναι αριθμοί μπορούν να συγκριθούν μεταξύ τους κα να διαταχθούν σε σειρά (αύξουσα ή φθίνουσα).
- Για να μπορέσω να συγκρίνω δύο ή περισσότερα κλάσματα πρέπει να έχουν τον ίδιο αριθμητή ή τον ίδιο παρονομαστή.
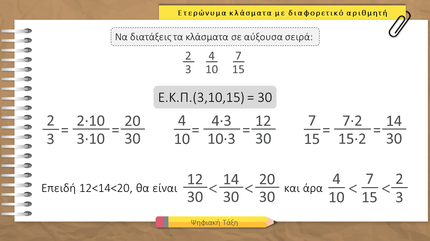
- Για να συγκρίνω δύο κλάσματα που έχουν διαφορετικούς και τους αριθμητές και τους παρονομαστές τους, πρέπει να τα κάνω ομώνυμα.
Ετερώνυμα κλάσματα με διαφορετικό αριθμητή
-
1ος τρόπος
-
2ος τρόπος
<
>
Μετατρέπουμε τα ετερώνυμα κλάσματα σε ομώνυμα και τα συγκρίνουμε. Για να φρεσκάρεις τη μνήμη σου κοίταξε εδώ πώς γίνεται η μετατροπή.
εξασκηση
εκπαιδευτικο σεναριο
φυλλα εργασιασ
Προβλήματα με πρόσθεση και αφαίρεση κλασμάτων
Για να προσθέσω ή αφαιρέσω κλάσματα, θα πρέπει αυτά να είναι ομώνυμα και τότε προσθέτω ή αφαιρώ αντίστοιχα τους αριθμητές τους.
Για να λύσω ένα πρόβλημα που τα δεδομένα του βρίσκονται σε διαφορετικές μορφές (φυσικοί, δεκαδικοί, κλασματικοί, μεικτοί αριθμοί), ακολουθώ τα παρακάτω βήματα:
- 1ο βήμα: Μετρατρέπω όλα τα δεδομένα στην ίδια μορφή.
- 2ο βήμα: Εκτελώ τις πράξεις σύμφωνα με όσα λέει το πρόβλημα.
- 3ο βήμα: Ελέγχω αν το αποτέλεσμα που βρήκα είναι λογικό.
|
Τα παιδιά των τάξεων Δ΄, Ε΄και Στ΄ σε ένα δημοτικό σχολείο αποφάσισαν να διοργανώσουν μια δίωρη χριστουγεννιάτικη γιορτή. Ο διαθέσιμος χρόνος μοιράστηκε:
Περισσεύει χρόνος για να παρουσιάσουν και ένα κοινό πρόγραμμα οι τρεις τάξεις; Αν ναι, πόσα λεπτά είναι;
|
λυση προβληματοσ
- Πρέπει να προσθέσω τον χρόνο των μαθητών: 1/3 + 3/10 + 1/4
- Παρατηρώ όμως πως είναι ετερώνυμα οπότε θα τα κάνω ομώνυμα.
- Γνωρίζοντας πως η μία ώρα έχει 60 λεπτά θα κάνω τα κλάσματα ομώνυμα με παρονομαστή το 60.
- Συνεπώς 1/3 + 3/10 + 1/4 = 20/60 + 18/60 + 15/60 = 53/60
- Άρα στην μία ώρα έχουμε 60/60 - 53/60 = 7/60. Περισσεύουν 7 λεπτά στη μία ώρα.
- Στο δίωρο θα έχουμε 7 + 7 = 14 λεπτά για κοινό πρόγραμμα.
Προβλήματα με πολλαπλασιασμό και διαίρεση κλασμάτων
|
4. Για να υπολογίσω αριθμητικές παραστάσεις που περιέχουν κλασματικούς αριθμούς, πρώτα μετατρέπω, αν χρειάζεται, κάποιους από τους αριθμούς σε άλλη μορφή. Στην συνέχεια εκτελούμε τις πράξεις από αριστερά προς τα δεξιά, με τη γνωστή σειρά (παρενθέσεις, πολλαπλασιασμοί και διαιρέσεις, προσθέσεις κι αφαιρέσεις).
|
φυλλα εργασιασ