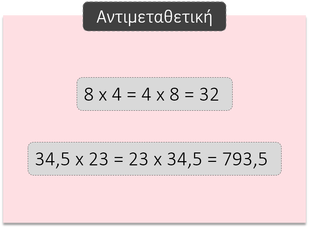​Μαθήματα ενότητας

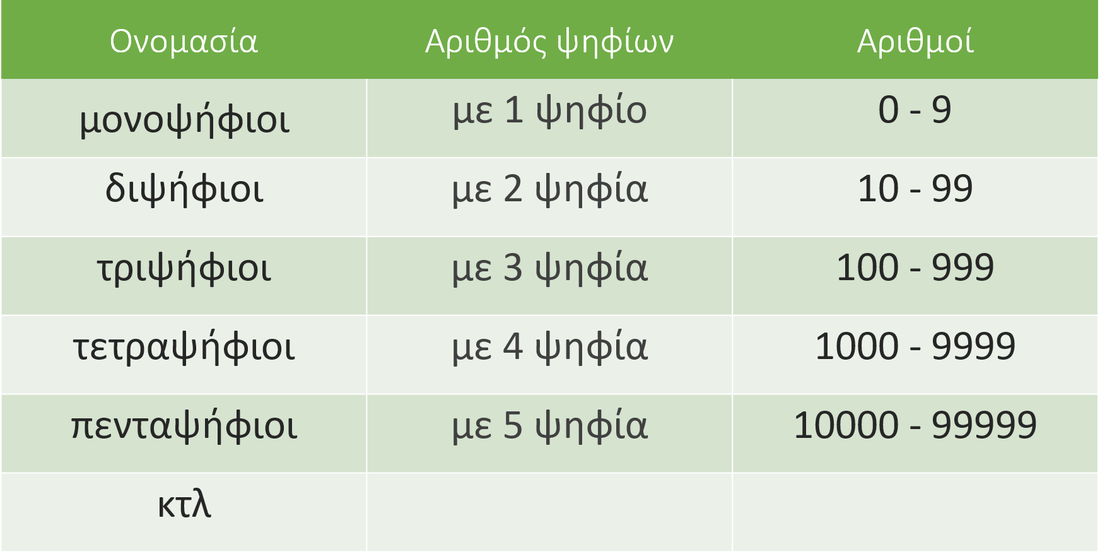
  • Φυσικοί αριθμοί
  • Δεκαδικοί αριθμοί
  • ​Μετατροπή δεκαδικών σε κλάσματα κι αντίστροφα
  • Σύγκριση φυσικών ή δεκαδικών αριθμών
  • Πρόσθεση και αφαίρεση φυσικών και δεκαδικών αριθμών
  • Πολλαπλασιασμός φυσικών και δεκαδικών αριθμών
  • Διαίρεση φυσικών και δεκαδικών αριθμών​
  • Πράξεις με μεικτές αριθμητικές παραστάσεις

Φυσικοί αριθμοί

Φυσικοί αριθμοί

Λέγονται οι αριθμοί που βρίσκονται καθημερινά στη φύση, γύρω μας.
  • 1 τραπέζι, 4 μπάλες, 35 άτομα, 130 κιβώτια, 1.000 χιλιόμετρα κλπ.
Εκτός από πλήθος οι αριθμοί αυτοί μπορούν να δηλώσουν και τη θέση – σειρά που μπορεί να βρίσκεται κάποιος.
  • στη σειρά είμαι 5ος, κάθομαι στο 7ο θρανίο, πηγαίνω στο 8ο Δ.Σ. κλπ. 
Οι φυσικοί  αριθμοί που αρχίζουν από το 0 και φτάνουν στο ...άπειρο
(0,1,2,3,4,5,6...)
Όλοι οι φυσικοί αριθμοί σχηματίζονται από 10 ψηφία
  • (0,1,2,3,4,5,6,7,8,9)
Κάθε φυσικός αριθμός έχει έναν επόμενο και έναν προηγούμενο φυσικό αριθμό, εκτός από το 0 που έχει μόνο επόμενο, το 1.
  • 17 + 1 = 18
Στους αριθμούς που έχουν περισσότερα από τρία ψηφία, για λόγους ευκολίας στην ανάγνωση, χωρίζουμε με μία τελεία κάθε τριάδα ψηφίων, αρχίζοντας από τις μονάδες (δεξιά).
  • Για παράδειγμα ο αριθμός 4578965 χρησιμοποιώντας τις τελείες διαχωρισμού θα γραφεί ως εξής: 4.578.965

Δεκαδικοί αριθμοί

Δεκαδικοί αριθμοί

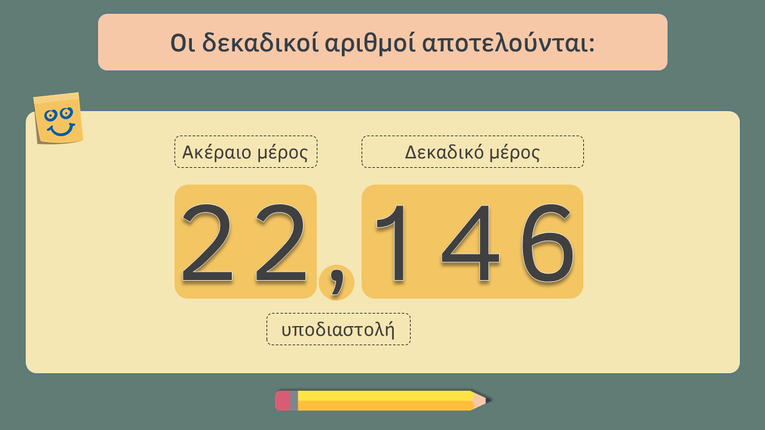
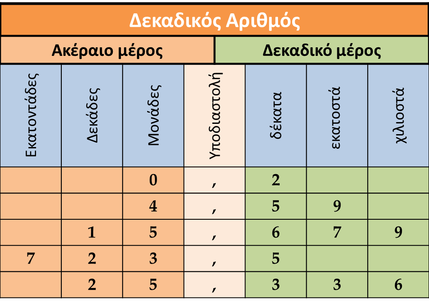
Όταν στην καθημερινή ζωή θέλουμε να εκφράσουμε ένα μέγεθος με ακρίβεια, τότε χρησιμοποιούμε τους δεκαδικούς αριθμούς. Οι αριθμοί αυτοί περιέχουν το ακέραιο μέρος ενός αριθμού και το δεκαδικό μέρος του. Ο χωρισμός ακέραιου και δεκαδικού μέρους γίνεται με την υποδιαστολή (κόμμα).
π.χ. 1 λίτρο βενζίνης κοστίζει 1,568 ευρώ
  • Στο ακέραιο μέρος, τα ψηφία ανάλογα με τη θέση τους μπορεί να δηλώνουν Μονάδες (Μ), Δεκάδες (Δ), Εκατοντάδες (Ε) 
  • Στο δεκαδικό μέρος τα ψηφία μπορεί να δηλώνουν δέκατα (δεκ.), εκατοστά (εκ.), χιλιοστά (χιλ.) 
  • Η αξία ενός δεκαδικού αριθμού δεν αλλάζει αν προσθέσουμε ή διαγράψουμε μηδενικά από το τέλος του δεκαδικού αριθμού
Προσοχή! Δεν διαγράφουμε ποτέ μηδενικά από το τέλος του ακεραίου αριθμού.
εξασκηση 1
εξασκηση 2

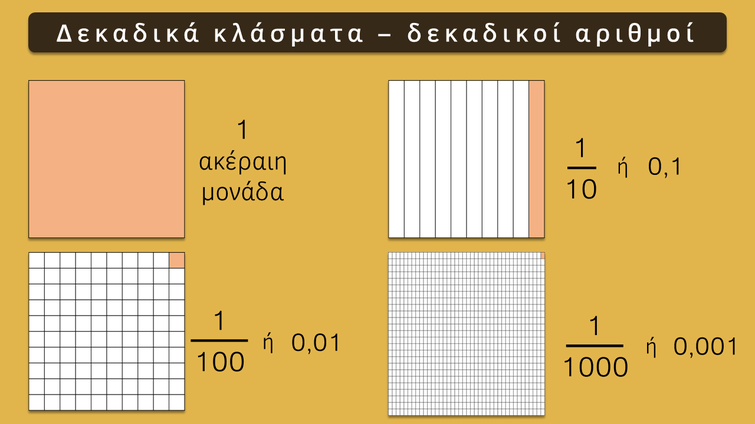
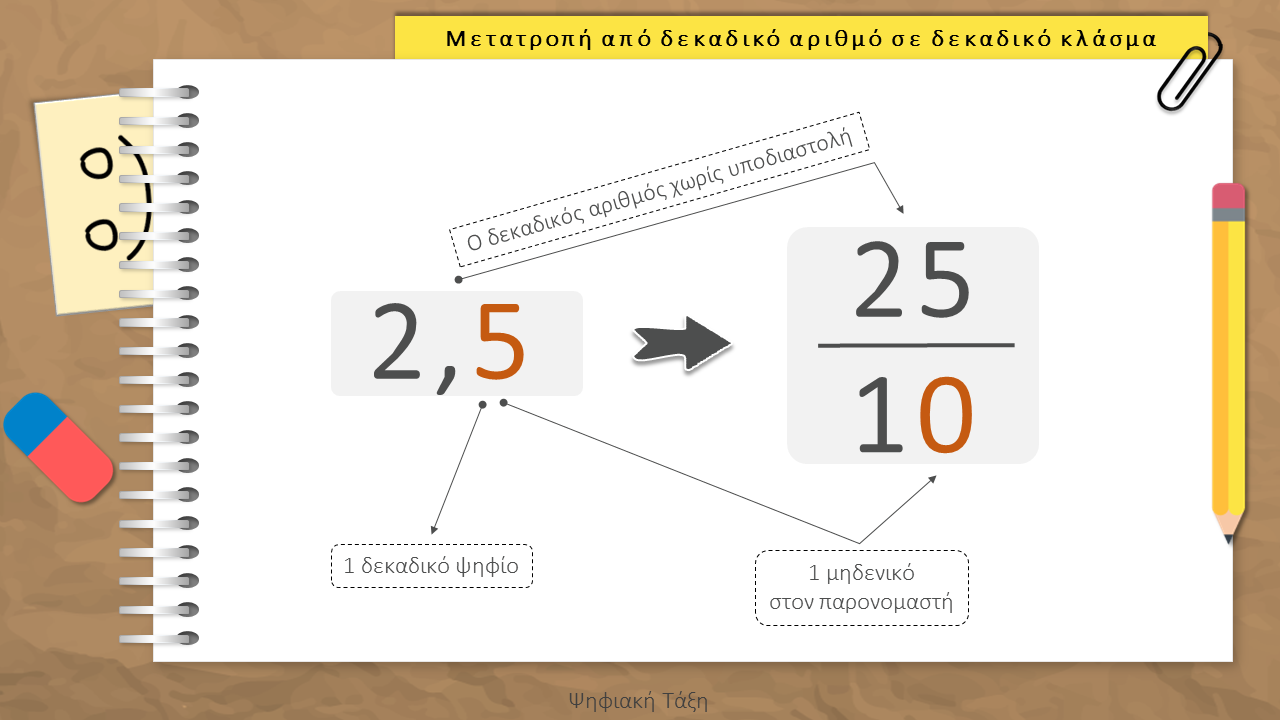
Μετατροπή δεκαδικών σε κλάσματα και αντίστροφα

Μετατροπή δεκαδικών σε κλάσματα και αντίστροφα

Οι δεκαδικοί αριθμοί μπορούν να μετατραπούν σε δεκαδικά κλάσματα και, αντίστροφα, τα δεκαδικά κλάσματα να μετατραπούν σε δεκαδικούς αριθμούς.
  • 1η
  • 2η
<
>
Για να μετατρέψουμε ένα δεκαδικό αριθμό  σε κλάσμα:
  • Γράφουμε ολόκληρο τον αριθμό, χωρίς την υποδιαστολή, στη θέση του αριθμητή.
  • Στη θέση του παρονομαστή γράφουμε τον αριθμό 1, με τόσα μηδενικά όσα ήταν τα δεκαδικά ψηφία του αριθμού.
Για να μετατρέψουμε ένα δεκαδικό κλάσμα σε δεκαδικό αριθμό:
  • Γράφουμε μόνο τον αριθμητή του.
  • Χωρίζουμε με υποδιαστολή, από τα δεξιά προς τ’ αριστερά, τόσα δεκαδικά ψηφία όσα μηδενικά έχει ο παρονομαστής του.
εξασκηση 1
εξασκηση 2
φυλλα εργασιασ

Σύγκριση φυσικών ή δεκαδικών αριθμών

Σύγκριση φυσικών ή δεκαδικών αριθμών

Η σύγκριση δύο αριθμών δείχνει ποιος από τους δύο είναι ο μεγαλύτερος, ποιος είναι ο μικρότερος ή αν είναι ίσοι. Τα σύμβολα που χρησιμοποιώ για εκφράσω το αποτέλεσμα μιας σύγκρισης είναι:
• < είναι μικρότερο
• = είναι ίσο
• > είναι μεγαλύτερο
Παραδείγματα
​7 < 10
14,2 = 14,2
5,12 > 4,40
Η σύγκριση και η διάταξη των αριθμών μας επιτρέπει να παρεμβάλουμε έναν ή περισσότερους αριθμούς ανάμεσα σε δύο άλλους.
Παραδείγματα
​Ανάμεσα στους αριθμούς 7 και 8 μπορώ να παρεμβάλω τους αριθμούς: 7,1 / 7,2 / 7,3 κτλ.
  • Αύξουσα διάταξη
  • Φθίνουσα διάταξη
<
>
Όταν θέλουμε να διατάξουμε ορισμένους αριθμούς κατά αύξουσα σειρά, τους γράφουμε σε μία γραμμή, αρχίζοντας από τον μικρότερο προς τον με­γαλύτερο.
Όταν θέλουμε να τους διατάξουμε κατά φθίνουσα σειρά, τους γράφου­με σε μία σειρά, ξεκινώντας από τον μεγαλύτερο και φτάνοντας στον μικρό­τερο.
εξασκηση 1
εξασκηση 2
φυλλα εργασιασ

Πρόσθεση και αφαίρεση φυσικών και δεκαδικών αριθμών

Πρόσθεση και αφαίρεση φυσικών και δεκαδικών αριθμών

Το αποτέλεσμα μιας πρόσθεσης λέγεται την άθροισμα. Το αποτέλεσμα μιας αφαίρεσης λέγεται διαφορά.
Η πρόσθεση έχει τις παρακάτω ιδιότητες:
  • ​Αντιμεταθετική
  • ​Προσεταιριστική
<
>
Αντιμεταθετική ιδιότητα: Αν αλλάξουμε τη σειρά των προσθετέων, το αποτέλεσμα της πρόσθεσης δεν αλλάζει.
Προσεταιριστική ιδιότητα: Για να προσθέσουμε πολλούς αριθμούς, προσθέτουμε τους δύο πρώτους, στο άθροισμά τους προσθέτουμε τον τρίτο, στο νέο άθροισμα προσθέτουμε τον τέταρτο κ.ο.κ. Αν αλλάξουμε τα ζευγάρια των προσθετέων, το άθροισμά τους δε μεταβάλλεται.
Οι πράξεις της πρόσθεσης της αφαίρεσης είναι πράξεις αντίστροφες, γιατί:
  • Μια πρόσθεση...
  • Μια αφαίρεση...
  • ΠΡΟΣΟΧΗ!
<
>
Μια πρόσθεση μπορεί να είναι η δοκιμή της αφαίρεσης.
Μια αφαίρεση να είναι η δοκιμή της πρόσθεσης.
  • Στην κάθετη πρόσθεση και την αφαίρεση δεκαδικών αριθμών, οι υποδιαστολές μπαίνουν η μία κάτω από την άλλη. Έτσι τα δέκατα είναι κάτω από τα δέκατα, τα εκατοστά κάτω από τα εκατοστά κτλ.
  • Στην κάθετη πρόσθεση ή αφαίρεση δεκαδικών αριθμών, αν οι δεκαδικοί δεν έχουν το ίδιο πλήθος δεκαδικών ψηφίων, για να μη μπερδεύομαι, προσθέτω μηδενικά στο δεκαδικό τους μέρος, έτσι ώστε όλοι να έχουν το ίδιο πλήθος δεκαδικών ψηφίων.

Πολλαπλασιασμός φυσικών και δεκαδικών αριθμών

Πολλαπλασιασμός φυσικών και δεκαδικών αριθμών

Οι δύο ιδιότητες της πρόσθεσης ισχύουν και στον πολλαπλασιασμό των φυσικών και των δεκαδικών αριθμών: Η αντιμεταθετική ιδιότητα, η προσεταιριστική ιδιότητα  και ακόμη μια ιδιότητα , η επιμεριστική.
  • Αντιμεταθετική
  • Προσεταιριστική
  • Επιμεριστική
  • Θυμάμαι
  • ​ΠΡΟΣΟΧΗ!
<
>
Αντιμεταθετική ιδιότητα: 
Αν αλλάξουμε τη σειρά των παραγόντων ενός γινομένου, το αποτέλεσμα του πολλαπλασιασμού δεν αλλάζει. 
Προσεταιριστική ιδιότητα: 
Αν σε ένα γινόμενο τριών ή περισσότερων παραγόντων αντί να πολλαπλασιάσουμε τον πρώτο με το δεύτερο αριθμό και το αποτέλεσμα με τον τρίτο, πολλαπλασιάσουμε πρώτα το δεύτερο με τον τρίτο και το αποτέλεσμα με τον πρώτο, το τελικό αποτέλεσμα δεν αλλάζει.
Επιμεριστική ιδιότητα:
Όταν θέλουμε να πολλαπλασιάσουμε έναν αριθμό με ένα άθροισμα δύο ή περισσότερων προσθετέων, μπορούμε να πολλαπλασιάσουμε τον αριθμό με κάθε προσθετέο και να προσθέσουμε τα επί μέρους γινόμενα. Η επιμεριστική ιδιότητα του πολλαπλασιασμού ισχύει και ως προς την αφαίρεση.
1. Για να πολλαπλασιάσουμε ένα φυσικό αριθμό με 10, 100 ή 1000, γράφουμε τον αριθμό και προσθέτουμε στο τέλος τόσα μηδενικά όσα έχει το 10, το 100 ή το 1000.
  • 7 Χ 1.000 = 7.000

2. Για να πολλαπλασιάσουμε ένα δεκαδικό αριθμό με 10, 100 ή 1000, μετακινούμε την υποδιαστολή τόσες θέσεις δεξιά όσα είναι τα μηδενικά του 10, του 100 ή του 1000. Αν δεν φτάσουν, συμπληρώνουμε με μηδενικά.
  • 2,513 Χ 100 = 251,3     

3. Για να πολλαπλασιάσουμε έναν ακέραιο αριθμό με 0,1 ή 0,01 ή 0,001 κ.ο.κ., χωρίζουμε από το τέλος του αριθμού με υποδιαστολή ένα, δύο, τρία κ.ο.κ. ψηφία.
  • 632 Χ 0,01 = 6,32

4. Ο πολλαπλασιασμός ενός αριθμού με μηδέν δίνει πάντα αποτέλεσμα μηδέν.
  • 0 Χ 345 = 0

5. Ο πολλαπλασιασμός ενός αριθμού με το 1 δίνει πάντα γινόμενο τον ίδιο τον αριθμό.
  • 1 Χ 345 = 345
Στον πολλαπλασιασμό δεκαδικών αριθμών, το πλήθος των δεκαδικών ψηφίων του γινομένου είναι ίσο με το άθροισμα των δεκαδικών ψηφίων των παραγόντων του.

Ο Πυθαγόρας και ο Πυθαγόρειος πίνακας

Στην αρχαία Ελλάδα ζούσε ο Πυθαγόρας, μεγάλος φιλόσοφος και μαθηματικός.  Γεννήθηκε σε χρονολογία που δεν μας είναι γνωστή, αλλά που εικάζεται πως είναι το 570 π.Χ. και ως επικρατέστερος τόπος γεννήσεως φέρεται η νήσος Σάμος. Είχε εφεύρει έναν «πίνακα», όπως τον έλεγε, που διευκόλυνε τους πολλαπλασιασμούς, οι οποίοι έως τότε γίνονταν με το μυαλό ή απλούστερα με πετραδάκια.
Μας φαίνεται τόσο απλό πράγμα! Ωστόσο, ο Πυθαγόρας αφιέρωσε είκοσι ολόκληρα χρόνια της ζωής του, ώσπου να επινοήσει αυτόν τον πίνακα, ο οποίος έκανε αθάνατο το όνομά του στους κατοπινούς αιώνες.

Διαίρεση φυσικών και δεκαδικών αριθμών​

Διαίρεση φυσικών και δεκαδικών αριθμών​

Διαίρεση λέγεται η πράξη με την οποία μοιράζουμε έναν αριθμό σε τόσα ίσα μέρη, όσα μας λέει ένας άλλος αριθμός.
Έχουμε δυο ειδών διαιρέσεις :
  • Τη διαίρεση μερισμού. Όταν ξέρουμε την τιμή των πολλών μονάδων και ζητάμε την τιμή της μιας μονάδας.
        Π.χ. Οι πέντε σοκολάτες κοστίζουν 7,5 €. Πόσο κοστίζει η μία ;
  • Τη διαίρεση μέτρησης. Όταν ξέρουμε και την τιμή των πολλών μονάδων και την τιμή της μιας μονάδας και δεν ξέρουμε πόσες είναι αυτές οι πολλές μονάδες.
        Π.χ. Αν έχω 12 κιλά μέλι και γεμίσω βάζα των 2 κιλών το καθένα. Πόσα βάζα χρησιμοποίησα;
  • Διαίρεση
  • Μαθαίνω
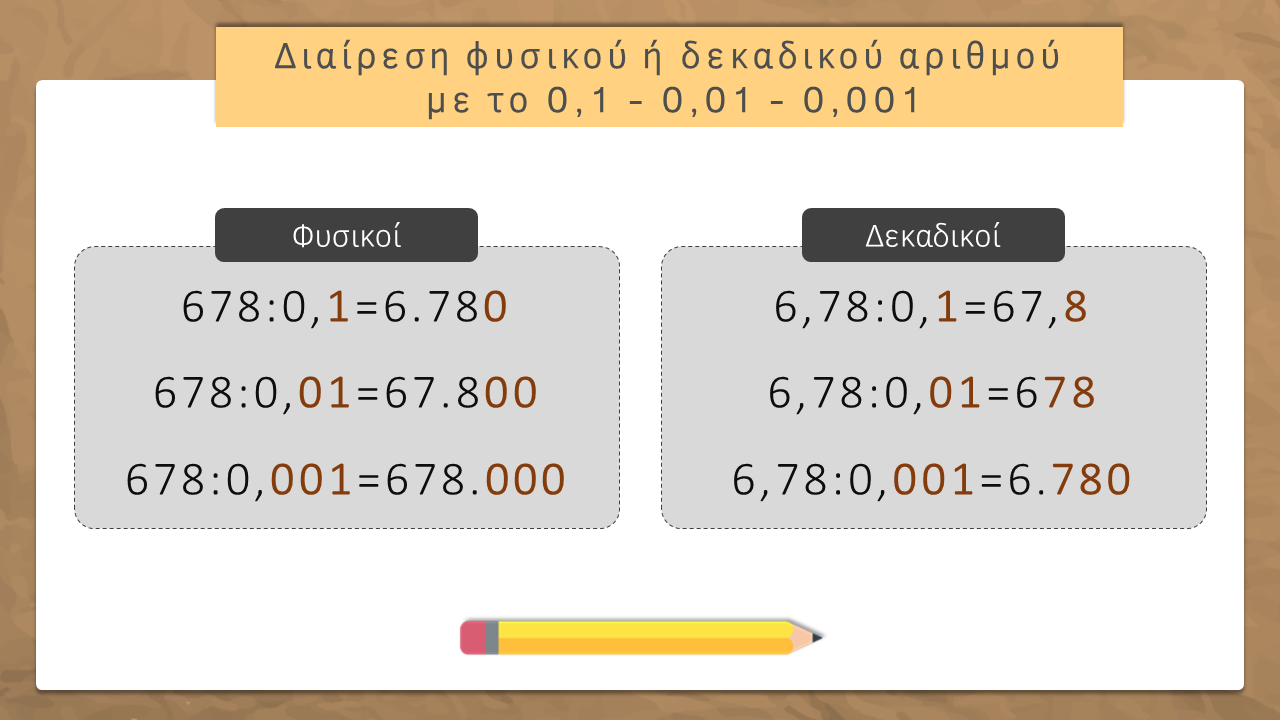
  • Διαίρεση με το 0,1 , 0,01 , 0,001
<
>
Δοκιμή διαίρεσης
Σε κάθε διαίρεση ο διαιρετέος είναι ίσος με το γινόμενο του διαιρέτη επί το πη­λίκο συν  το υπόλοιπο. Αυτή είναι η δοκιμή (ή επαλήθευση) της διαίρεσης.
  • Κάθε αριθμός αν διαιρεθεί με το 1, δίνει πηλίκο τον εαυτό του. 
​      π.χ. 5 : 1 = 5
  • Κάθε αριθμός αν διαιρεθεί με τον εαυτό του δίνει πηλίκο το 1.
      π.χ. 9 : 9 = 1
  • Το μηδέν (0) με όποιον αριθμό κι αν διαιρεθεί, δίνει πηλίκο τον εαυτό του.
​     π.χ. 0 : 5 = 0
  • Δεν επιτρέπεται να διαιρέσουμε έναν αριθμό δια μηδέν (0).
​     π.χ. 4 : 0 είναι αδύνατο
  • ​Σε κάθε διαίρεση αν πολλαπλασιάσουμε ή διαιρέσουμε τους δύο όρους με τον ίδιο αριθμό, το πηλίκο δεν αλλάζει.    
      π.χ. 20 : 4 = 5 (20 • 2) : (4 • 2) = 40 : 8 = 5
  • Όταν διαιρώ έναν αριθμό με 0,1 , 0,01 κτλ ο αριθμός μεγαλώνει, 10, 100, 1.000 φορές.
  • Για να διαιρέσω ένα φυσικό αριθμό με το 0,1, το 0,01, το 0,001..., προσθέτω στον αριθμό ένα, δύο ή τρία... μηδενικά αντίστοιχα.
  • Για να διαιρέσω ένα δεκαδικό αριθμό με το 0,1, το 0,01, το 0,001..., μεταφέρω την υποδιαστολή του αριθμού δεξιά μία, δύο ή τρεις... θέσεις αντίστοιχα. Αν τελειώσουν τα ψηφία του αριθμού, βάζω μηδενικά.

Πράξεις με μεικτές αριθμητικές παραστάσεις

Πράξεις με μεικτές αριθμητικές παραστάσεις

Όταν μια σειρά αριθμών συνδέονται μεταξύ τους με τα σύμβολα των πράξεων (+ - Χ :), λέμε ότι έχουμε αριθμητική παράσταση.
π.χ. 3 + 5 • 6 - 12 : 4
Οι πράξεις σε μια αριθμητική παράσταση γίνονται από αριστερά προς τα δεξιά:
  • Πρώτα γίνονται οι πολλαπλασιασμοί και οι διαιρέσεις.
  • Ακολουθούν οι προσθέσεις και οι αφαιρέσεις.
  • Αν υπάρχουν παρενθέσεις πρώτα γίνονται οι πράξεις μέσα στις παρενθέσεις με την ίδια σειρά (πρώτα πολλαπλασιασμοί και διαιρέσεις και μετά προσθέσεις και αφαιρέσεις). 
  • Αν έχουμε συνεχόμενους πολλαπλασιασμούς και διαιρέσεις ή συνεχόμενες προσθέσεις και αφαιρέσεις, οι πράξεις γίνονται με τη σειρά που βρίσκονται στην αριθμητική παράσταση.
φυλλα εργασιασ