​Μαθήματα ενότητας

  • Λύνω σύνθετα προβλήματα των 4 πράξεων
  • Η χρήση του υπολογιστή τσέπης
  • Στρογγυλοποίηση φυσικών και δεκαδικών αριθμών
  • Διαιρέτες ενός αριθμού - Μ.Κ.Δ. Αριθμών
  • Κριτήρια διαιρετότητας
  • Πρώτοι και σύνθετοι αριθμοί
  • Παραγοντοποίηση φυσικών αριθμών
  • Πολλαπλάσια ενός αριθμού - Ε.Κ.Π​

Λύνω σύνθετα προβλήματα των 4 πράξεων

Λύνω τα παρακάτω προβλήματα

​Ένα μικρό φορτηγό άδειο ζυγίζει 2,58 τόνους. Οι εργάτες στην αποθήκη το φόρτωσαν με κιβώτια βάρους 56 κιλών το καθένα και τώρα φορτωμένο ζυγίζει 6.780 κιλά.
  • ​Πόσα ήταν τα κιβώτια που φόρτωσαν οι εργάτες στο φορτηγό;
λυση του προβληματοσ
Δεδομένα
Λύση
Άδειο: 2,58 τόνοι = 2.580 κιλά
Το συνολικό βάρος των 56 κιβωτίων είναι
Γεμάτο: 6.780 κιλά
6.780 - 2.580 = 4.200
Βάρος 1 κιβωτίου: 56 κιλά
-
Ζητούμενα
Άρα, τα κιβώτια που φορτώθηκαν ήταν
Αριθμός κιβωτίων;
4.200 : 56 = 75
​​Η κυρία Μαρία έχει τρία εγγόνια, τον Πέτρο, τον Παντελή και την Αλίκη. Τους έδωσε 110 ευρώ και τους είπε να τα μοιραστούν, έτσι ώστε ο Παντελής να πάρει 10 ευρώ περισσότερα από τον Πέτρο, αλλά 15 ευρώ λιγότερα από την Αλίκη.  
  • ​Να βοηθήσεις τα τρία παιδιά να μοιραστούν σωστά τα χρήματα της γιαγιάς τους. 
λυση του προβληματος
Δεδομένα
Λύση
110 ευρώ για μοίρασμα
​Ο Πέτρος και η Αλίκη θα πάρουν το ίδιο ποσό με τον Παντελή αν στο αρχικό ποσό προσθέσουμε επιπλέον 10 ευρώ του Παντελή και αφαιρέσουμε 15 ευρώ της Αλίκης.
Παντελής (+ 10) από Πέτρο
110+10=120
Παντελής (- 15) ​ από Αλίκη
120-15=105
Μοιράζω
Μοιράζω στα τρία παιδιά το ποσό 105:3=35
Ζητούμενα
​Άρα έχουμε για κάθε παιδί:
​Το ποσό κάθε παιδιού
Παντελής: 35   Πέτρος: 35-10=25   Αλίκη: 35+15=50   ​

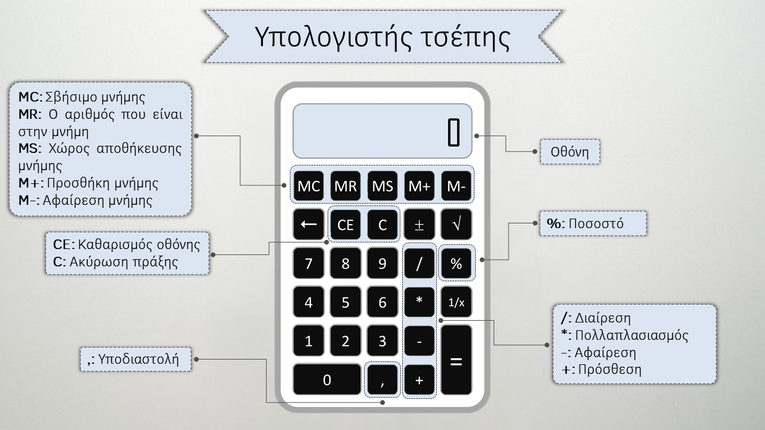
Η χρήση του υπολογιστή τσέπης

Η χρήση του υπολογιστή τσέπης

Πότε χρησιμοποιούμε τον υπολογιστή τσέπης;
  • ​Τον χρησιμοποιούμε: για να πραγματοποιούμε γρήγορα μεγάλους υπολογισμούς για να κάνουμε γρήγορα επαλήθευση των αποτελεσμάτων μας.
Τι είδους υπολογιστή τσέπης διαλέγουμε;
  • Διαλέγουμε υπολογιστή απλό και εύχρηστο Αποφεύγουμε κάποιον με χαρακτηριστικά που δεν μας χρειάζονται.
Ποια είναι τα όρια ενός υπολογιστή τσέπης;
  • Σ’ έναν υπολογιστή τσέπης η οθόνη «χωράει» συνήθως 8 ή 9 ψηφία Δεν μπορεί να επεξεργαστεί αριθμούς με περισσότερα ψηφία από αυτά.

Στρογγυλοποίηση φυσικών και δεκαδικών αριθμών

Στρογγυλοποίηση φυσικών και δεκαδικών αριθμών

  • Πότε κάνουμε στρογγυλοποίηση σε έναν αριθμό και γιατί;
Κάνουμε στρογγυλοποίηση σε έναν αριθμό, φυσικό ή δεκαδικό, όταν θέλουμε να θυμόμαστε εύκολα τον αριθμό ή όταν θέλουμε να κάνουμε πράξεις υπολογίζοντας το αποτέλεσμα γρήγορα, αλλά χωρίς ακρίβεια.
​
  • Πώς κάνουμε, λοιπόν, στρογγυλοποίηση;
Η διαδικασία της στρογγυλοποίησης είναι ίδια για τους φυσικούς και για τους δεκαδικούς αριθμούς και είναι η εξής:
α) Επιλέγουμε το ψηφίο του αριθμού στο οποίο θα κάνουμε στρογγυλοποίηση 
β) Παρατηρούμε το ψηφίο που βρίσκεται δεξιά του
  1. Αν αυτό το ψηφίο στα δεξιά είναι 0 ή 1 ή 2 ή 3 ή 4 (δηλαδή λιγότερο από 5), τότε από εκεί κι έπειτα όλα τα ψηφία μηδενίζονται και το ψηφίο στο οποίο κάναμε στρογγυλοποίηση καθώς και όλα τα μπροστινά του τα ξαναγράφουμε όπως είναι.
  2. Αν όμως το ψηφίο στα δεξιά είναι 5 ή 6 ή 7 ή 8 ή 9 (δηλαδή από 5 και πάνω), τότε από εκεί κι έπειτα όλα τα ψηφία μηδενίζονται ενώ το ψηφίο της στρογγυλοποίησης αυξάνεται κατά μία μονάδα.
εξασκηση
φυλλα εργασιασ

Διαιρέτες ενός αριθμού - Μ.Κ.Δ. Αριθμών

​Διαιρέτες ενός αριθμού - Μ.Κ.Δ. Αριθμών

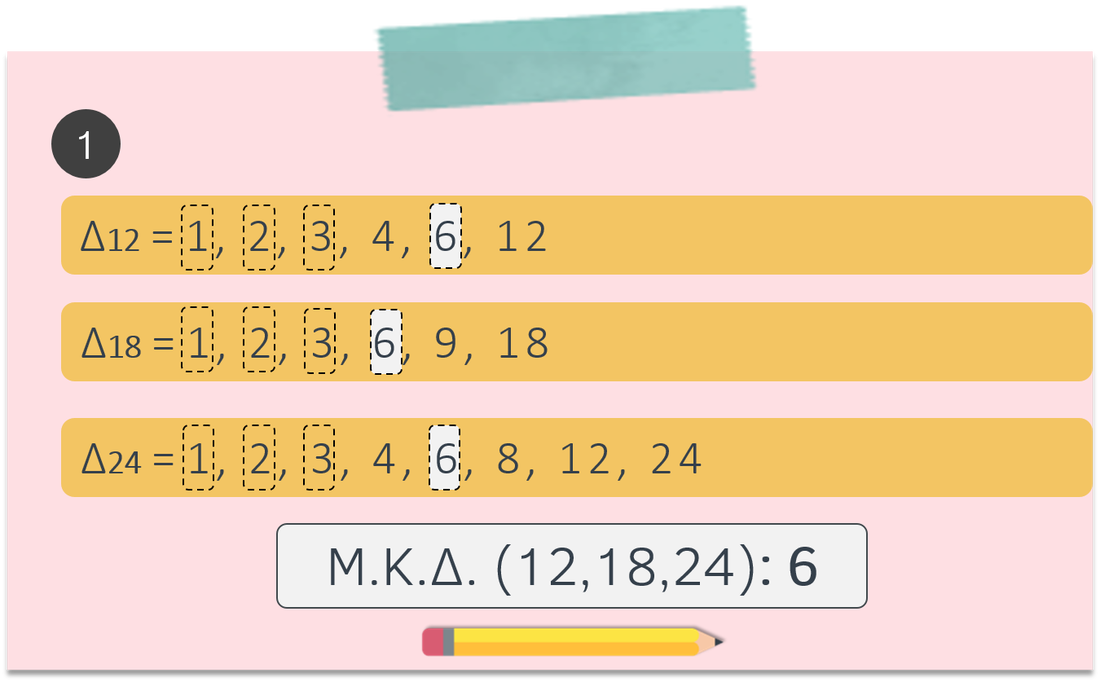
Διαιρέτης ενός φυσικού αριθμού είναι κάθε άλλος αριθμός φυσικός αριθμός που τον διαιρεί τέλεια. Ο αριθμός 12 έχει διαιρέτες τους αριθμούς 1, 2, 3, 4, 6, 12.
  • Όλοι οι φυσικοί αριθμοί έχουν διαιρέτες τουλάχιστον το 1 και τον εαυτό τους.
  • Ένας αριθμός μπορεί να έχει πολλούς διαιρέτες.
  • Υπάρχουν αριθμοί που κάποιοι από τους διαιρέτες που έχουν είναι ίδιοι. Λέμε τότε ότι έχουν κοινούς διαιρέτες.
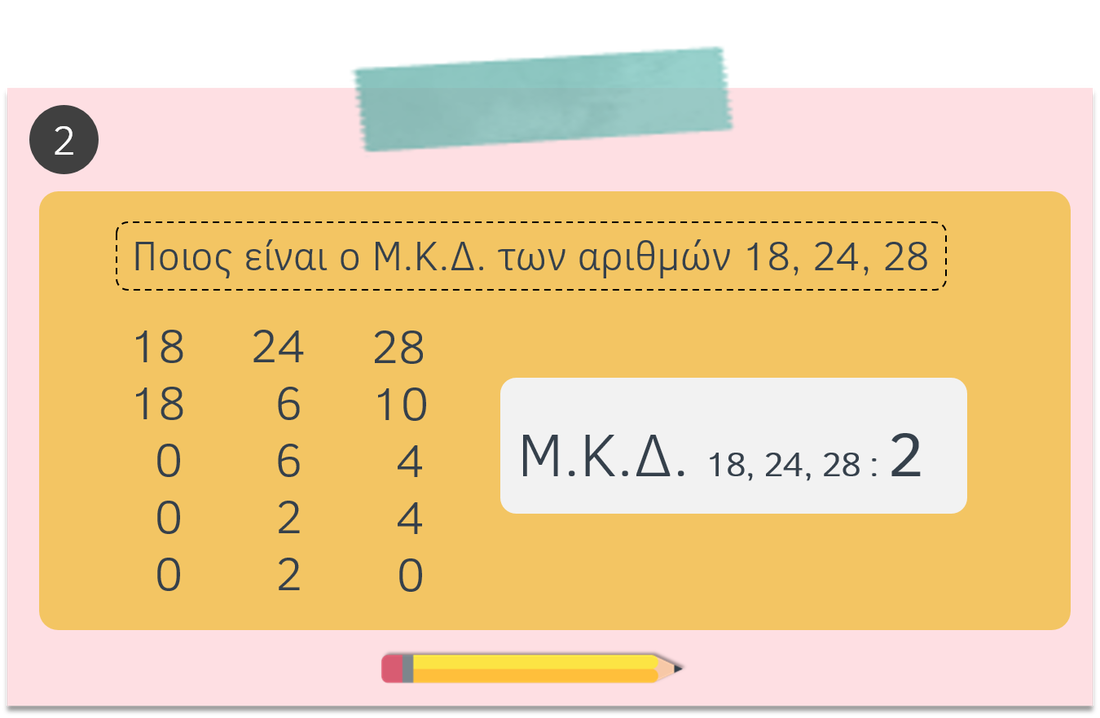
Μέγιστος Κοινός Διαιρέτης (Μ.Κ.Δ.) δύο ή περισσότερων αριθμών είναι ο μεγαλύτερος από τους κοινούς διαιρέτες των αριθμών αυτών.

Πώς βρίσκουμε το Μ.Κ.Δ.

  • 1ος τρόπος
  • 2ος τρόπος
<
>
  • Βρίσκω τους διαιρέτες των αριθμών 12, 18 και 24.
  • Ξεχωρίζω τους κοινούς διαιρέτες: 1, 2, 3, και 6.
  • Ο μεγαλύτερος από τους κοινούς διαιρέτες (Μ.Κ.Δ.) είναι ο αριθμός 6.
  • Γράφω τους αριθμούς σε οριζόντια διάταξη, κατεβάζω το μικρότερο απ’ αυτούς (18) και τους διαιρώ με αυτόν.
  • Κάτω από κάθε αριθμό από τους άλλους γράφω το αντίστοιχο υπόλοιπο από τη διαίρεσή του (δηλαδή 6 κάτω από το 24 και 10 κάτω από το 28).
  • Κατεβάζω πάλι το μικρότερο από τους αριθμούς στη 2η σειρά τώρα (6) και διαιρώ τους υπόλοιπους με αυτόν.
  • Όταν μείνει μόνο ένας αριθμός και οι υπόλοιποι είναι 0, αυτός είναι ο Μ.Κ.Δ. Έτσι έχουμε Μ.Κ.Δ. (18, 24, 28) = 2
φυλλα εργασιασ

Κριτήρια διαιρετότητας

Κριτήρια διαιρετότητας

Ένα κριτήριο διαιρετότητας είναι ένας κανόνας που μας βοηθάει να διακρίνουμε αν ένας αριθμός διαιρείται (τέλεια) η όχι με κάποιον άλλον αριθμό. Ένα κριτήριο διαιρετότητας δε βρίσκει το πηλίκο μιας διαίρεσης.
  • του 2
  • του 3
  • του 5
  • του 9
  • του 10,100,1000
  • του 4
  • του 25
<
>
Ένας αριθμός διαιρείται με το 2 αν το τελευταίο ψηφίο είναι άρτιος (ζυγός) αριθμός (0,2,4,6,8). 
​Ένας αριθμός διαιρείται με το 3, αν το μονοψήφιο άθροισμα των ψηφίων του είναι 3, 6 ή 9.
​Ένας αριθμός διαιρείται με το 5 αν το τελευταίο ψηφίο είναι 0 ή 5.   
​ Ένας αριθμός διαιρείται με το 9 αν το μονοψήφιο άθροισμα των ψηφίων του είναι το 9.
​Ένας αριθμός διαιρείται με το:
  • το 10 όταν τελειώνει σε ένα τουλάχιστον 0
  • το 100 όταν τελειώνει σε δύο τουλάχιστον 0
  • το 1.000 όταν τελειώνει σε τρία τουλάχιστον 0
​Ένας αριθμός διαιρείται με το 4 αν ο αριθμός που σχηματίζεται από τα δύο τελευταία ψηφία του διαιρείται με το 4.
Ένας αριθμός διαιρείται με το 25, αν το τελευταίο διψήφιο τμήμα του είναι 00, ή 25, ή 50, ή 75.

Πρώτοι και σύνθετοι αριθμοί

Πρώτοι και σύνθετοι αριθμοί

Πρώτοι
Ένας αριθμός, μεγαλύτερος από το 1, που έχει μόνο δύο διαιρέτες (το 1 και τον εαυτό του) λέγεται πρώτος.
Παράδειγμα
  • Ο αριθμός 2, έχει για διαιρέτες μόνο το 1 και το 2.
  • Ο αριθμός 7, έχει για διαιρέτες μόνο το 1 και το 7.
Σύνθετοι
Ένας αριθμός που έχει τουλάχιστον τρεις διαιρέτες λέγεται σύνθετος.
Παράδειγμα
  • Ο αριθμός  6, έχει για διαιρέτες το 1, το 2 και το 3
  • Ο αριθμός  8, έχει για διαιρέτες το 1, το 2 και το 4
Ο αριθμός 1 δεν είναι ούτε πρώτος ούτε σύνθετος (έχει μόνο έναν διαιρέτη, τον εαυτό του).

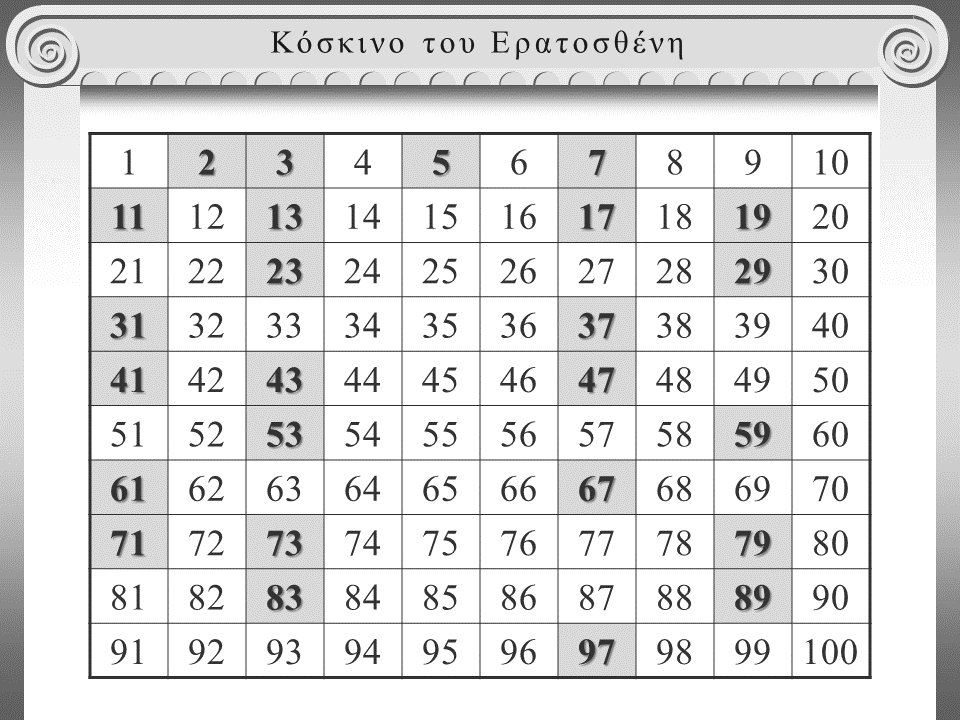
Κόσκινο του Ερατοσθένη

Οι αρχαίοι Έλληνες γνώριζαν ότι δεν υπάρχει μέγιστος πρώτος αριθμός, δηλαδή ότι οι πρώτοι αριθμοί είναι άπειροι στο πλήθος. Γνώριζαν ακόμη ότι δεν υπάρχει ένας απλός κανόνας που να δίνει τους διαδοχικούς πρώτους αριθμούς.
​Με την απλή μέθοδο του Ερατοσθένη, γνωστή ως "Κόσκινο του Ερατοσθένη", που χρησιμοποιείται μέχρι και σήμερα, βρίσκουμε όλους τους πρώτους αριθμούς που είναι μικρότεροι από δοσμένο αριθμό.
Οι πρώτοι αριθμοί μέχρι το 100

Μπορούμε να βρούμε τους πρώτους αριθμούς μέχρι το 100 με το «κόσκινο του Ερα­τοσθένη». Το «κόσκινο» που επινόησε ξεχωρίζει τους αριθμούς που έχουν μόνο δύο διαιρέτες από τους υπόλοιπους. Να πώς λειτουργεί:
  • Διαγράφουμε τον αριθμό 1.
  • Διαγράφουμε τα πολλαπλάσια του 2 εκτός από το 2.
  • Διαγράφουμε τα πολλαπλάσια του 3 εκτός από το 3.
  • Διαγράφουμε τα πολλαπλάσια του 5 εκτός από το 5.
  • Διαγράφουμε τα πολλαπλάσια του 7 εκτός από το 7.
  • Κυκλώνουμε τους 25 αριθμούς που απέμειναν. Είναι οι πρώτοι αριθμοί μέχρι το 100.
κοσκινο του ερατοσθενη
Βρες τους πρωτους αριθμους ως το 100
​Επίλεξε το “Show multiples” ή “Hide multiples”. Έπειτα κάνε κλικ στο 2, το 3, το 5 και το 7 , ώστε να επιλεγούν (ή διαγραφούν) τα πολλαπλάσιά τους .
εξασκηση

Παραγοντοποίηση φυσικών αριθμών

Παραγοντοποίηση φυσικών αριθμών

  • Τι είναι;
  • Ποιοι αριθμοί;
  • Πώς γίνεται;
  • 1ος
  • 2ος
<
>
Κάθε σύνθετος αριθμός μπορεί να γραφτεί σε παραγοντοποιημένη μορφή, δηλαδή σαν γινόμενο πρώτων παραγόντων.
  • Ο αριθμός 60 γράφεται: 2 Χ 2 Χ 3 Χ 5
Μόνο οι σύνθετοι αριθμοί παραγοντοποιούνται. Ένας πρώτος αριθμός δεν μπορεί να γραφτεί σε παραγοντοποιημένη μορφή, γιατί γράφεται μόνο ως γινόμενο του ​1 επί τον εαυτό του.
  • Ο αριθμός 91 (πρώτος αριθμός) μπορεί να γραφτεί ως 1 Χ 91
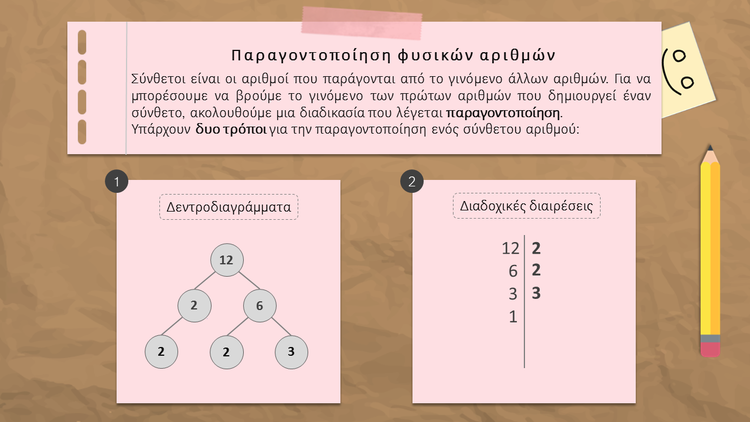
Μπορούμε να αναλύσουμε ένα σύνθετο αριθμό σε γινόμενο πρώτων παραγόντων...
  • με δεντροδιαγράμματα ή
  • με διαδοχικές διαιρέσεις

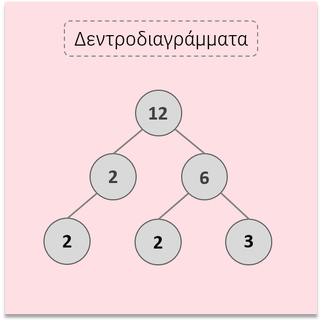
Δεντροδιαγράμματα

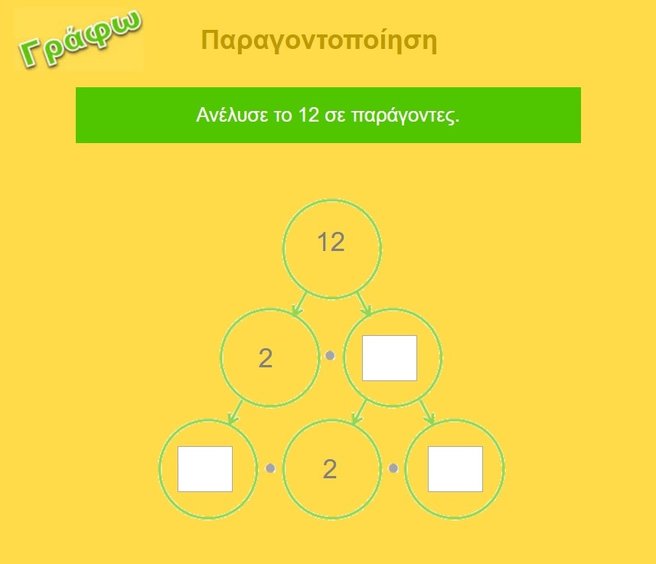
Γράφουμε το γινόμενο που μας δίνει τον αριθμό 12. Εδώ γράψαμε 2 Χ 6.
Ο αριθμός 2 είναι πρώτος, οπότε συνεχίζουμε τη διαδικασία για τον αριθμό 6, του οποίου το γινόμενο είναι 2 Χ 3.
Στην τρίτη σειρά γράφουμε τον αριθμό 2 και το γινόμενο 2 Χ 3.
Η ανάλυση τελειώνει, όταν όλοι οι παράγοντες είναι πρώτοι αριθμοί όπως εδώ (2, 2 και 3).
Άρα ο αριθμός 12 μπορεί να εκφραστεί ως γινόμενο πρώτων παραγόντων ως εξής: 12 = 2 Χ 2 Χ 3

Διαδοχικές διαιρέσεις

1. Εξετάζουμε ποιος είναι ο μικρότερος πρώτος αριθμός που διαιρεί ακριβώς το 12. Είναι το 2. Διαιρούμε με το 2 και γράφουμε κάτω από το 6 το πηλίκο της διαίρεσης.
2. Συνεχίζουμε την ίδια διαδικασία για το 6. Διαιρούμε με το 2 και γράφουμε το πηλίκο της διαίρεσης που είναι το 3.
3. Το 3 δε διαιρείται με το 2. Πάμε στον επόμενο πρώτο αριθμό που είναι το 3 και εξετάζουμε αν διαιρείται με το 3. Διαιρούμε με το 3 και γράφουμε το πηλίκο της διαίρεσης που είναι το 1. 4. Αν το πηλίκο είναι η μονάδα τότε τελειώνει και η ανάλυση.
Άρα ο αριθμός 12 εκφράζεται ως γινόμενο πρώτων παραγόντων ως εξής: 12 = 2 Χ 2 Χ 3
εξασκηση 1
  • Κάνε κλικ στην εικόνα.
  • ​Διάλεξε έναν αριθμό και κάνε κλικ στο κάθε φύλλο για να δεις την ανάλυση σε γινόμενο πρώτων παραγόντων.
εξασκηση 2
Κάνε κλικ στην εικόνα.

Πολλαπλάσια ενός αριθμού - Ε.Κ.Π​

Πολλαπλάσια ενός αριθμού - Ε.Κ.Π

Πολλαπλάσια ενός αριθμού είναι οι αριθμοί που προκύπτουν (δημιουργούνται) όταν πολλαπλασιάσουμε το συγκεκριμένο αριθμό με οποιοδήποτε ακέραιο αριθμό.
Παράδειγμα:
Τα πολλαπλάσια του 4 είναι το 4, 8, 12, 16…
​4x2=8, 4x3=12, 4x4=16
Τα πολλαπλάσια κάθε αριθμού είναι άπειρα, διότι άπειροι είναι και οι αριθμοί με τους οποίους μπορώ να τον πολλαπλασιάσω.
Κοινά πολλαπλάσια (Κ.Π.) δύο ή περισσότερων αριθμών είναι τα πολλαπλάσια τα οποία είναι ίδια σε όλους τους αριθμούς
Παράδειγμα:
Π3 = 3, 6, 9, 12, 15, 18, 21, 24, 27, ...
Π4 = 4, 8, 12, 16, 20, 24, 28, ...
Π6 = 6, 12, 18, 24, 30, ...
Τα κοινά πολλαπλάσια του 3 του 4 και του 6, που είναι μικρότερα από το 30, είναι τα 12, 24.
​Ελάχιστο Κοινό Πολλαπλάσιο (Ε.Κ.Π.) δύο ή περισσότερων αριθμών είναι το μικρότερο (ελάχιστο) από τα κοινά πολλαπλάσια των αριθμών.

Πώς βρίσκουμε το Ε.Κ.Π. δύο ή περισσότερων αριθμών

  • 1ος τρόπος
  • 2ος τρόπος
  • 3ος τρόπος
<
>
  • Βρίσκουμε μερικά πολλαπλάσια των αριθμών.
  • Σημειώνουμε τα κοινά πολλαπλάσιά τους.
  • Επιλέγουμε το μικρότερο από αυτά.
​Παίρνουμε τον μεγαλύτερο αριθμό. Εξετάζουμε αν είναι πολλαπλάσιο ταυτόχρονα των άλλων. Εάν είναι, αυτός είναι και το Ε.Κ.Π.
Εάν δεν είναι, παίρνουμε τον διπλάσιό του και εξετάζουμε το ίδιο πράγμα.
Εάν δεν είναι και πάλι πολλαπλάσιο των άλλων, παίρνουμε τον τριπλάσιό του και ελέγχουμε ξανά. Συνεχίζουμε με τον ίδιο τρόπο, μέχρι να βρούμε ένα πολλαπλάσιο του μεγαλύτερου αριθμού που να είναι πολλαπλάσιο ταυτόχρονα και των άλλων αριθμών. Αυτό θα είναι και το Ε.Κ.Π.
  • Γράφω οριζόντια τους αριθμούς και δεξιά τους φέρνω μια κατακόρυφη γραμμή.
  • Δεξιά της γραμμής γράφω πρώτους αριθμούς (2,3,5,7,11…) που διαιρούν έστω και έναν από τους αριθμούς που έχουν δοθεί.
  • Τότε αριστερά της γραμμής, κάτω από τους αριθμούς που έχουν δοθεί, βάζω τα πηλίκα (όταν η διαίρεση είναι τέλεια) ή τον ίδιο αριθμό (όταν η διαίρεση δεν είναι τέλεια).
  • Συνεχίζω την ίδια διαδικασία μέχρι όλα τα πηλίκα να γίνουν 1.
  • Έτσι καταλήγουμε σε μια νέα γραμμή που όλα τα πηλίκα είναι μονάδες. Το Ε.Κ.Π. είναι το γινόμενο των αριθμών που βρίσκονται δεξιά της κατακόρυφης γραμμής