Από το βιβλίο που αποσύρθηκε
Μαθήματα ενότητας
- Υπενθύμιση ύλης Δ' Τάξης
- Υπενθύμιση - οι αριθμοί μέχρι το 1.000.000
- Οι αριθμοί μέχρι το 1.000.000.000
- Αξία θέσης ψηφίου στους μεγάλους αριθμούς
- Υπολογισμοί με μεγάλους αριθμούς
- Επίλυση προβλημάτων
Υπενθύμιση Δ΄ τάξης
Βασικά σημεία θεωρίας
|
1. Όταν κάνουμε πράξεις, μπορούμε να εκτιμήσουμε γρήγορα το αποτέλεσμα αντικαθιστώντας τους αριθμούς με κοντινούς «στρόγγυλους» αριθμούς. Όσο πιο κοντά είναι οι στρόγγυλοι στους αρχικούς αριθμούς, τόσο μεγαλύτερη ακρίβεια εξασφαλίζουμε στις εκτιμήσεις μας.
Παράδειγμα
72+56=70+60=130 (128) 79+61=80+60=140 |
2. Για να επιλύσουμε ένα πρόβλημα, είναι απαραίτητο να αξιολογούμε σωστά και να οργανώνουμε τις πληροφορίες που μας δίνονται (άγνωστα – γνωστά). Αν δεν μπορούμε να το λύσουμε το ζωγραφίζουμε ή αντικαθιστούμε τους αριθμούς με άλλους μικρότερους για να βρούμε τι πράξεις πρέπει να κάνουμε. Συχνά, για να απαντήσουμε στο ερώτημα ενός προβλήματος είναι απαραίτητο να βρίσκουμε και να απαντούμε στα «κρυφά» ερωτήματα. Υπάρχουν προβλήματα που έχουν παραπάνω από μία λύσεις.
|
|
3. Όταν ξέρουμε την τιμή της μονάδας μπορούμε να βρούμε την τιμή για οποιαδήποτε άλλη ποσότητα.
Παράδειγμα
Τα 4 τετράδια κοστίζουν 120 λεπτά. Πόσο κοστίζουν τα 2 τετράδια;
|
4. Για να συνεχίσουμε ένα μοτίβο πρέπει να ανακαλύψουμε τον κανόνα τον οποίο ακολουθεί.
Παράδειγμα
3 – 6 – 9 - ? Ο επόμενος αριθμός είναι το 12 αφού ο κανόνας είναι: ο προηγούμενος αριθμός + 3 |
|
5. Ένα σχήμα μπορεί να έχει έναν αλλά και περισσότερους άξονες συμμετρίας. Τα συμμετρικά μέρη έχουν ίση περίμετρο και ίσο εμβαδόν μεταξύ τους.
Παράδειγμα
|
6. Για να υπολογίσουμε την περίμετρο ενός σχήματος, προσθέτουμε τα μήκη όλων των πλευρών του.
Παράδειγμα
Π = 14+23+14+23 =74 μ. |
7. Για να υπολογίσουμε το εμβαδόν του τετραγώνου και του ορθογωνίου παραλληλογράμμου πολλαπλασιάζουμε τα μήκη δυο διαδοχικών πλευρών του (αν το σχήμα είναι σύνθετο, το χωρίζουμε σε γνωστά σχήματα και βρίσκουμε τα επιμέρους εμβαδά κι έπειτα τα προσθέτουμε).
Παράδειγμα
|
εμβαδόν = μήκος Χ πλάτος
4 Χ 3 = 12 |
Υπενθύμιση - οι αριθμοί μέχρι το 1.000.000
Υπενθύμιση - οι αριθμοί μέχρι το 1.000.000
Ένας αριθμός μπορεί να γραφεί με τρεις διαφορετικούς τρόπους :
1) Μπορεί να γραφεί με ψηφία (π.χ. 46.500)
2) Με λέξεις (π.χ. σαράντα έξι χιλιάδες πεντακόσια)
3) Με μεικτό τρόπο, με ψηφία και με λέξεις (π.χ. 46 χιλιάδες 500).
1) Μπορεί να γραφεί με ψηφία (π.χ. 46.500)
2) Με λέξεις (π.χ. σαράντα έξι χιλιάδες πεντακόσια)
3) Με μεικτό τρόπο, με ψηφία και με λέξεις (π.χ. 46 χιλιάδες 500).
Σε έναν αριθμό κάθε ψηφίο έχει διαφορετική αξία ανάλογα με τη θέση του. Στον παρακάτω πίνακα βλέπουμε την αξία κάθε ψηφίου ανάλογα με τη θέση που έχει στον αριθμό.
Παράδειγμα
Οι αριθμοί μέχρι το 1.000.000
|
Οι αριθμοί ανάλογα με το πλήθος των ψηφίων τους χωρίζουμε σε :
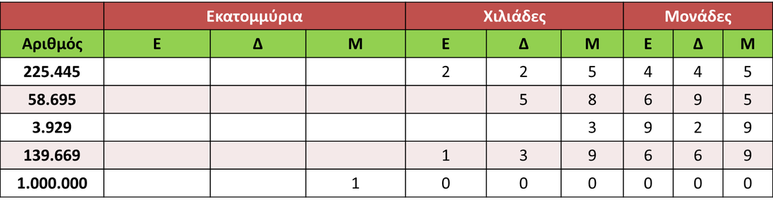
Πώς μπορώ να αναλύσω έναν αριθμό;
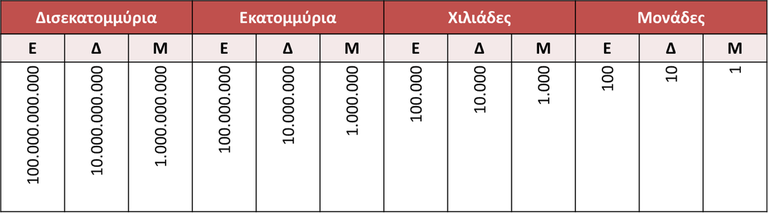
Κάθε αριθμός αναλύεται στο περιεχόμενο του κάθε ψηφίου του. Για να κάνω ανάλυση ενός αριθμού γράφω κάθε ψηφίο του με τόσα μηδενικά δεξιά του, όσες είναι και οι θέσεις των ψηφίων δεξιά. |
|
συμπερασμα
Μπορώ να γράψω έναν αριθμό:
Μπορώ να γράψω έναν αριθμό στον πίνακα, τοποθετώντας κάθε ψηφίο του αριθμού στην αντίστοιχη με την αξία του θέση.
- Με λέξεις: τριακόσιες πενήντα χιλιάδες
- Με ψηφία: 350.000
- Με ψηφία και με λέξεις (μεικτή γραφή): 350 χιλιάδες
Μπορώ να γράψω έναν αριθμό στον πίνακα, τοποθετώντας κάθε ψηφίο του αριθμού στην αντίστοιχη με την αξία του θέση.
Η ΑΡΙΘΜΟΓΡΑΜΜΗ
Κάνε κλικ στο New number για να ξεκινήσεις. Στόχος σου είναι να βρεις σταδιακά τον αριθμό πηγαίνοντας
από γραμμή σε γραμμή. οι αριθμογραμμές μετακινούνται δεξιά και αριστερά με το ποντίκι. Καλή διασκέδαση.
από γραμμή σε γραμμή. οι αριθμογραμμές μετακινούνται δεξιά και αριστερά με το ποντίκι. Καλή διασκέδαση.
Οι αριθμοί μέχρι το 1.000.000.000
Χάρτης που απεικονίζει τον πληθυσμό της γης. Τα νούμερα αντιστοιχούν στα χρώματα πάνω στον χάρτη.
Οι αριθμοί μέχρι το 1.000.000.000
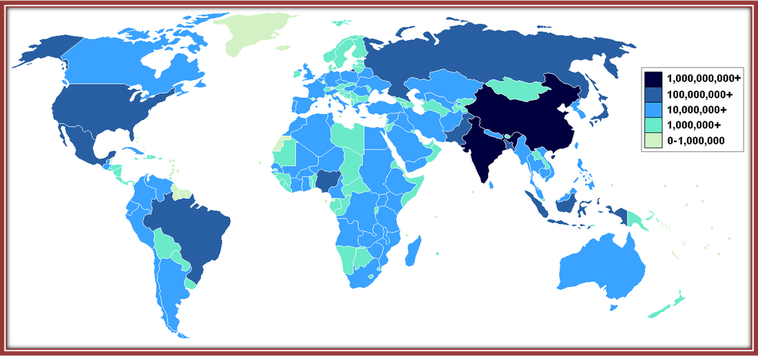
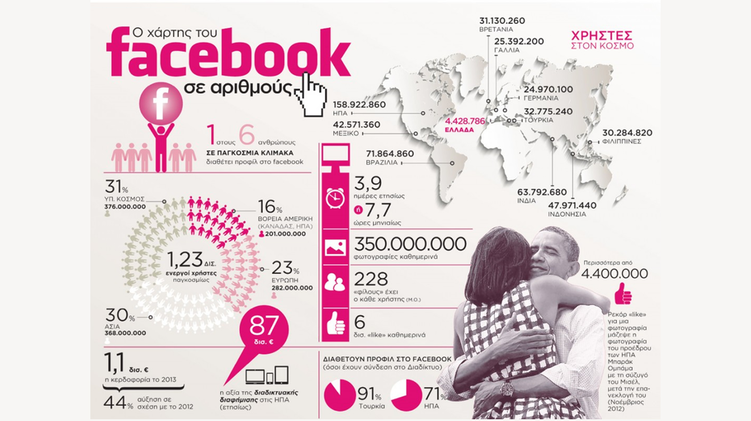
Ποιοι είναι οι αριθμοί με περισσότερα από 9 ψηφία;
Περισσότερα από εννέα (9) ψηφία έχουν οι αριθμοί που δείχνουν τον πληθυσμό ή την έκταση μιας χώρας, τις αποστάσεις των ουράνιων σωμάτων κ.λπ.
Αυτούς τους αριθμούς τους γράφουμε, όπως μάθαμε, είτε με αριθμητικά ψηφία είτε με λέξεις είτε με αριθμητικά ψηφία και λέξεις. Πιο εύκολος τρόπος για τόσο μεγάλους αριθμούς είναι να τους γράφουμε με ψηφία και λέξεις.
Αυτούς τους αριθμούς τους γράφουμε, όπως μάθαμε, είτε με αριθμητικά ψηφία είτε με λέξεις είτε με αριθμητικά ψηφία και λέξεις. Πιο εύκολος τρόπος για τόσο μεγάλους αριθμούς είναι να τους γράφουμε με ψηφία και λέξεις.
Η αξία κάθε ψηφίου στον αριθμό 450.367.982
συμπερασμα
Γράφουμε και διαβάζουμε μεγάλους αριθμούς εύκολα όταν χρησιμοποιούμε ψηφία και λέξεις (μεικτή γραφή).
Παραδείγματα:
325.000.000= 325 εκατ.
152.040.000= 152 εκατ. 40 χιλ. ή 152,04 εκατ.
325.000.000= 325 εκατ.
152.040.000= 152 εκατ. 40 χιλ. ή 152,04 εκατ.
ηλιακο συστημα - ενα ταξιδι αριθμων
Αξία θέσης ψηφίου στους μεγάλους αριθμούς
Αξία θέσης ψηφίου στους μεγάλους αριθμούς
Φυσικοί αριθμοί
Σύγκριση φυσικών αριθμών
|
Για να συγκρίνω δύο ή περισσότερους ακέραιους αριθμούς :
π.χ. 455 (τρία ψηφία), 45 (δύο ψηφία) 455 > 45
|
|
π.χ. 776 , 771
Οι Εκατοντάδες είναι ίσες, οι Δεκάδες είναι ίσες, στις Μονάδες το 6 είναι μεγαλύτερο από το 1 άρα : 776 > 771
|
|
|
συμπερασμα
Για να συγκρίνω δυο ακέραιους αριθμούς:
- Μετράω το πλήθος των ψηφίων τους (μεγαλύτερος είναι όποιος έχει περισσότερα ψηφία).
- Αν έχουν τον ίδιο αριθμό ψηφίων, συγκρίνω τα ψηφία ξεκινώντας από τη θέση με την μεγαλύτερη αξία.
Υπολογισμοί με μεγάλους αριθμούς
Υπολογισμοί με μεγάλους αριθμούς
|
Μερικές φορές, για να αντιληφθούμε ευκολότερα έναν αριθμό ή για να κάνουμε υπολογισμούς με το νου μας, τον στρογγυλοποιούμε. Η στρογγυλοποίηση μπορεί να γίνει σε διαφορετικά ψηφία του αριθμού, ανάλογα με την ακρίβεια που θέλουμε.
|
|
Στρογγυλοποίηση Φυσικών Αριθμών
- Βρίσκουμε το ψηφίο στο οποίο θέλουμε να γίνει η στρογγυλοποίηση.
- Κοιτάζουμε το ψηφίο που βρίσκεται δεξιά από αυτό στο οποίο θα κάνουμε στρογγυλοποίηση.
- Αν είναι 0 ή 1 ή 2 ή 3 ή 4 το ψηφίο της στρογγυλοποίησης θα μείνει το ίδιο ενώ όλα όσα βρίσκονται δεξιά του θα γίνουν 0.
- Αν είναι 5 ή 6 ή 7 ή 8 ή 9, τότε το ψηφίο της στρογγυλοποίησης αυξάνεται κατά 1 και όλα τα ψηφία που βρίσκονται δεξιά του θα γίνουν 0.
|
|
|
πινακασ πολλαπλασιασμου
Πίνακας πολλαπλασιασμού
|
|
Ο πολλαπλασιασμός είναι ένας γρήγορος τρόπος να κάνεις μια πρόσθεση που επαναλαμβάνεται ξανά και ξανά.
Πρόσθεση: 3 + 3 + 3 + 3 + 3 = 15 Πολλαπλασιασμός: 3 Χ 5 = 15
Στα πεναλτι - Εξασκηση στον πολλαπλασιασμο
Στα πέναλτι - Εξάσκηση στον πολλαπλασιασμό
συμπερασμα
Όταν κάνουμε υπολογισμούς με μεγάλους αριθμούς, μπορούμε να τους στρογγυλέψουμε και να βρούμε γρήγορα το αποτέλεσμα με εκτίμηση.
Παράδειγμα: 3.432.000 είναι περίπου 3.500.000 ή 3.400.000
Παράδειγμα: 3.432.000 είναι περίπου 3.500.000 ή 3.400.000
Επίλυση προβλημάτων
Πως λύνω ένα πρόβλημα
Για να λύσεις ένα πρόβλημα ασφαλώς να χρησιμοποιήσεις την σκέψη σου, τη φαντασία, τη μνήμη και την προσοχή. Με τη βοήθειά τους θα πετύχεις την κατανόησή του. Να γνωρίζεις βέβαια ότι κάθε μαθηματικό πρόβλημα κρύβει στις γραμμές του ένα ή περισσότερα ζητούμενα, δηλαδή άγνωστα στοιχεία. Σκοπός σου είναι να τα βρεις έχοντας οδηγούς σου τα γνωστά στοιχεία ή τις πληροφορίες που σου δίνει το πρόβλημα.
Λέξεις - φράσεις κλειδιά που μας οδηγούν στην επιλογή των σωστών πράξεων είναι:
- ΠΡΟΣΘΕΣΗ: παίρνω ακόμα, αυξάνω κατά, καταθέτω και, βάζω, θέλω ακόμη, ενώνω, συγκεντρώνω, εισπράττω κ.α.
- ΑΦΑΙΡΕΣΗ: δίνω, ξοδεύω, μου έμειναν, λιγοστεύω, μειώνω, ελαττώνω, διαφέρω κατά, συμπληρώνω, αδειάζω, αδυνατίζω, βγάζω, διαγράφω, καταναλώνω, έχω έκπτωση, υπόλοιπο κ.α.
- ΠΟΛΛΑΠΛΑΣΙΑΣΜΟΣ: πενταπλό, πέντε φορές μεγαλύτερο…, αν το 1 πράγμα έχει… πόσα έχουν 5 ίδια πράγματα;
- ΔΙΑΙΡΕΣΗ: μοιράζω, χωρίζω, τέμνω, κόβω σε… ίσα μέρη, κατανέμω ισότιμα, πόσες φορές χωράει…, πόσες συσκευασίες χρειάζονται…, πόσες ομάδες θα σχηματίσω… κ.α.
συμπερασμα
Η προσεκτική παρατήρηση και οργάνωση των δεδομένων και των ζητούμενων ενός προβλήματος μας βοηθάει να βρούμε ευκολότερα στρατηγικές που θα δώσουν τη λύση του.
Επανάληψη ενότητας
Εξάσκηση - Quiz
επαναληπτικες ασκησεις - φυλλα εργασιασ